



Next: ordinary point
Up: Definitions
Previous: order
For each point 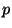 of a continuum
of a continuum  equipped with an
arc-structure
equipped with an
arc-structure
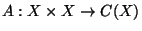 we define a partial
order
we define a partial
order 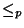 by letting
by letting 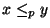 whenever
whenever
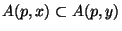 . Let
. Let  and
and 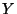 be continua with fixed
arc-structures
be continua with fixed
arc-structures 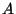 and
and 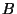 , respectively. We say that a
surjective mapping
, respectively. We say that a
surjective mapping
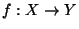 is a
is a 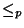 -mapping
provided that
-mapping
provided that 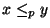 in
in  implies that
implies that
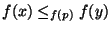 in
in 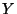 . If, in addition,
. If, in addition,
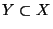 ,
,
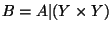 , and
, and 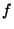 is a retraction, then
is a retraction, then 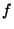 is
called a
is
called a 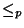 -retraction (or
-retraction (or 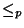 -preserving
retraction). The concept of a
-preserving
retraction). The concept of a 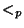 -mapping is
defined in a similar manner (with
-mapping is
defined in a similar manner (with
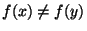 implied by
implied by
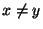 ). For order preserving mappings see e.g.
[Fugate et al. 1981, I.7, p. 553].
). For order preserving mappings see e.g.
[Fugate et al. 1981, I.7, p. 553].




Next: ordinary point
Up: Definitions
Previous: order
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30