



Next: order preserving mapping
Up: Definitions
Previous: orbit
Let 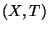 be a topological space, and let
be a topological space, and let
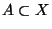 .
Let
.
Let 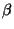 be a cardinal number. We say that
be a cardinal number. We say that 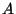 is of order less than equal to
is of order less than equal to 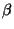 in
in  , written
ord(
, written
ord(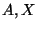 )
)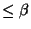 , provided that for each
, provided that for each 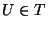 such
that
such
that
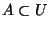 , there exists
, there exists 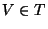 such that
such that
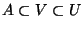 and
and
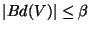 .
We say that
.
We say that 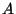 is of order
is of order 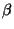 in
in  , written
ord(
, written
ord(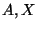 )
)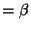 , provided that ord(
, provided that ord(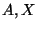 )
)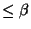 and
ord(
and
ord(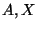 )
)
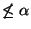 for any cardinal number
for any cardinal number
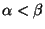 .
A concept of an order of a point
.
A concept of an order of a point 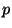 in a continuum
in a continuum  (in
the sense of Menger-Urysohn), written
(in
the sense of Menger-Urysohn), written
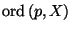 , is defined as follows.
Let
, is defined as follows.
Let
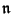 stand for a cardinal number. We write:
stand for a cardinal number. We write:
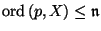 provided that for every
provided that for every
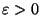 there is an
open neighborhood
there is an
open neighborhood  of
of 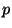 such that
such that
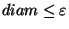 and
and
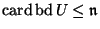 ;
;
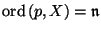 provided that
provided that
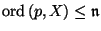 and
for each cardinal number
and
for each cardinal number
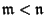 the condition
the condition
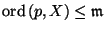 does not hold;
does not hold;
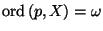 provided that the point
provided that the point 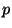 has arbitrarily small open
neighborhoods
has arbitrarily small open
neighborhoods 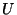 with finite boundaries
with finite boundaries
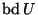 and
and
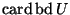 is not bounded by
any
is not bounded by
any
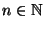 .
.
Thus, for any continuum  we have
we have
(convention:
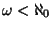 ); see [Kuratowski 1968, §51, I, p. 274].
Let a dendroid
); see [Kuratowski 1968, §51, I, p. 274].
Let a dendroid
 and a point
and a point 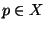 be given. Then
be given. Then 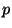 is said to be a
point of order at least
is said to be a
point of order at least
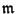 in the classical sense
provided that
in the classical sense
provided that 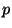 is
the center of an
is
the center of an
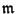 -od contained in
-od contained in  . We say that
. We say that 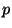 is a
point of order
is a
point of order
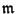 in the classical sense provided that
in the classical sense provided that
 is the minimum cardinality for which the above condition is
satisfied (see [Charatonik 1962, p. 229]).
is the minimum cardinality for which the above condition is
satisfied (see [Charatonik 1962, p. 229]).




Next: order preserving mapping
Up: Definitions
Previous: orbit
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() provided that for every
provided that for every
![]() there is an
open neighborhood
there is an
open neighborhood ![]() of
of ![]() such that
such that
![]() and
and
![]() ;
;
![]() provided that
provided that
![]() and
for each cardinal number
and
for each cardinal number
![]() the condition
the condition
![]() does not hold;
does not hold;
![]() provided that the point
provided that the point ![]() has arbitrarily small open
neighborhoods
has arbitrarily small open
neighborhoods ![]() with finite boundaries
with finite boundaries
![]() and
and
![]() is not bounded by
any
is not bounded by
any
![]() .
.
![]() we have
we have