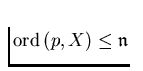 provided that for every
provided that for every
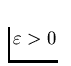 there is an
open neighborhood U of p such that
there is an
open neighborhood U of p such that
 and
and
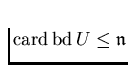 ;
;
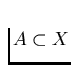 .
Let
.
Let 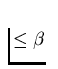 , provided that for each
, provided that for each 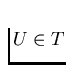 such
that
such
that 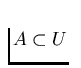 , there exists
, there exists 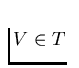 such that
such that
 and
and
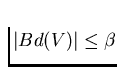 .
We say that A is of order
.
We say that A is of order 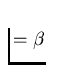 , provided that ord(A,X)
, provided that ord(A,X)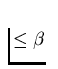 and
ord(A,X)
and
ord(A,X)
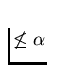 for any cardinal number
for any cardinal number
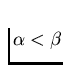 .
A concept of an order of a point p in a continuum X (in
the sense of Menger-Urysohn), written
.
A concept of an order of a point p in a continuum X (in
the sense of Menger-Urysohn), written
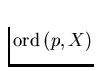 , is defined as follows.
Let
, is defined as follows.
Let
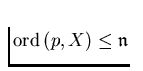 provided that for every
provided that for every
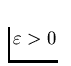 there is an
open neighborhood U of p such that
there is an
open neighborhood U of p such that
 and
and
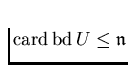 ;
;
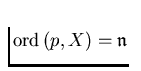 provided that
provided that
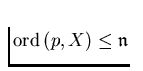 and
for each cardinal number
and
for each cardinal number
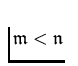 the condition
the condition
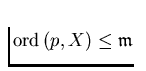 does not hold;
does not hold;
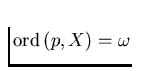 provided that the point p has arbitrarily small open
neighborhoods U with finite boundaries
provided that the point p has arbitrarily small open
neighborhoods U with finite boundaries
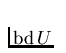 and
and
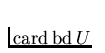 is not bounded by
any
is not bounded by
any
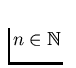 .
.
Thus, for any continuum X we have
 ); see [55, §51, I, p. 274].
Let a dendroid
X and a point
); see [55, §51, I, p. 274].
Let a dendroid
X and a point 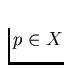 be given. Then p is said to be a
point of order at least
be given. Then p is said to be a
point of order at least