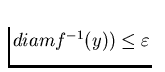 . If C is a
collection of continua, a continuum M is
C-like if, for every positive number
. If C is a
collection of continua, a continuum M is
C-like if, for every positive number 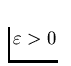 there is a tree T and a surjective
mapping
there is a tree T and a surjective
mapping 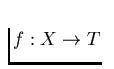 such that f is an
such that f is an 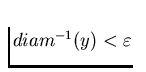 for each
for each 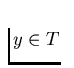 ). Let us mention that a continuum X is
tree-like if and only if it is the inverse limit of an inverse
sequence of trees with surjective bonding mappings. Compare e.g.
[65, p. 24].
Using a concept of a nerve of a covering, one can reformulate the above
definition saying that a continuum X is be tree-like provided that for each
). Let us mention that a continuum X is
tree-like if and only if it is the inverse limit of an inverse
sequence of trees with surjective bonding mappings. Compare e.g.
[65, p. 24].
Using a concept of a nerve of a covering, one can reformulate the above
definition saying that a continuum X is be tree-like provided that for each
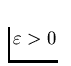 there is an
there is an Finally, the original definition using tree-chains can be found e.g. in Bing's paper [4, p. 653].