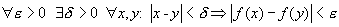
MAPLE
Stejnoměrně spojitá funkce
vs.
Lipschitzovská funkce
DEFINICE: Stejnoměrně spojitá funkce
Máme funkci f:R->R
Řekneme, že f je stejnoměrně spojitá, pokud pro každé fixní epsilon větší než nula, existuje jedno delta větší než nula, tak že pro všechna x,y na definičním oboru funkce musí pro toto jedno fixní epsilon platit:
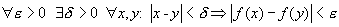
Od spojitosti se stejnoměrná spojitost liší v tom, že u spojitosti vezmeme
![]() a najdeme k němu
a najdeme k němu
![]() , které lze použít jen pro některá
x1,x2
.
, které lze použít jen pro některá
x1,x2
.
U stejnoměrné spojistosti musí jedno konkrétní
![]() existovat pro všechna
x
v celém definičním oboru funkce.
existovat pro všechna
x
v celém definičním oboru funkce.
![[Maple Plot]](images/spojitost10.gif)
|
Funkce x=y je stejnoměrně spojitá,protože pro každé epsilon má k sobě "přiměřeně velké" delta |
Funkce y=exp(x) není stejnoměrně spojitá na reálné ose, protože utíká příliš rychle k nekonečnu a my tak k fixnímu epsilon dostáváme stále menší a menší dela až se delta ztratí na nulu. |
Podmínka stejnoměrné spojitosti nám uzavírá graf funkce do "obdélníčku" ze kterého graf funkce nidky nesmí utéct směrem nahoru ani dolů.
![[Maple Plot]](images/spoj_obdelnicekcos.gif)
Funkce y=cos(x) je stejnoměrně spojitá, protože graf funkce nikdy neuteče z růžového obdélničku.
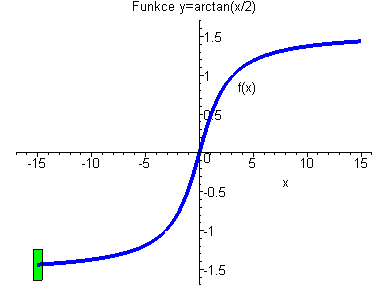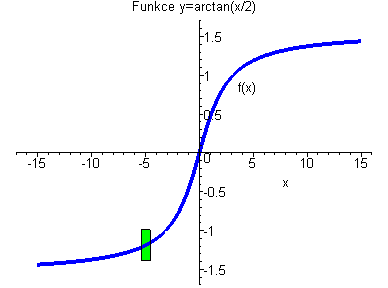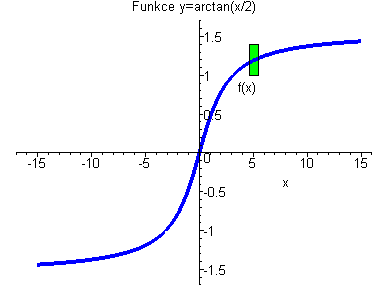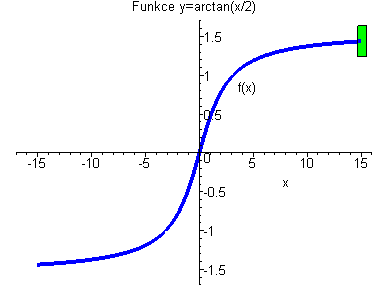 |
Funkce arctan(x/2) je stejnoměrně spojitá. Funkce nikdy neuteče ze zeleného obdélníčku. |
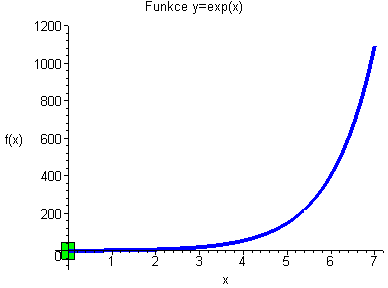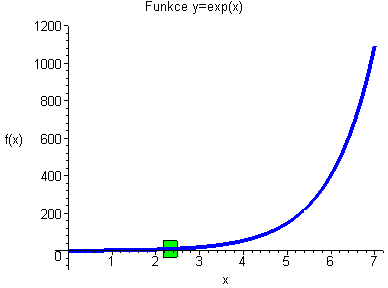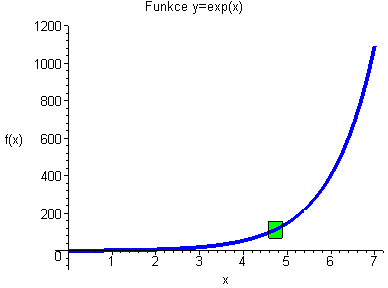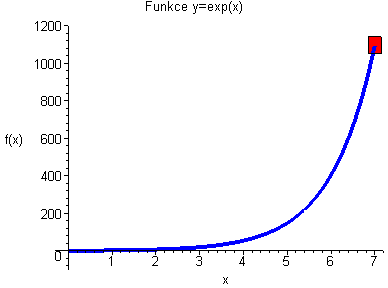 |
Funkce exp(x) není stejnoměrně spojitá, u nekonečna nám uteče ze zeleného obdélníčku. V tom momentě zelený obdélníček zčervená. |
DEFINICE: Lipschitzovská funkce
Funkce
f
je Lipschitzovská pokud
f
je spojitá a pokud existuje konstanta L>0 tak, že pro všechna
x1,x2
platí Lipschitzovská podmínka:
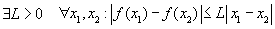
![[Maple Plot]](images/lip_cosx2.gif)
Konstatu L lze znázornit jako směrnici + L a - L (černá), kde graf funkce nesmí opustit růžový prostor mezi směrnicemi.
|
|
Graf funce exp(x) vždycky někde u nekonečna uteče z zelené oblasti směrnic. V tom momentě původní zelená oblast zčervená. |
|
|
Funkce
|
| y=x | y=exp(x) | y=x2 | y=x(1/2) | y=sin(x) |
|---|---|---|---|---|
| První derivace funkcí Pokud je první derivace omezená, tak funkce je Liptschitzovská. Vždy totiž existuje delta ostře větší než nula splňující Liptchitzovskou podmínku. |
||||
![[Maple Plot]](images/spojitost19.gif) |
![[Maple Plot]](images/spojitost22.gif) |
![[Maple Plot]](images/spojitost31.gif) |
![[Maple Plot]](images/spojitost35.gif) |
![[Maple Plot]](images/spojitost41.gif) |
Máme fixní epsilon , projíždíme s ním grafem funkce a díváme se na měnící se delta. |
||||
![[Maple Plot]](images/spojitost20.gif) |
![[Maple Plot]](images/spojitost21.gif) |
![[Maple Plot]](images/spojitost30.gif) |
![[Maple Plot]](images/spojitost34.gif) |
![[Maple Plot]](images/spojitost40.gif) |
Máme fixní epsilon, procházíme postupně osu y a díváme se jak velké je delta. |
||||
![[Maple Plot]](images/spojitost59.gif)
Funkce y=x je Lipschitzovská, protože máme konstantí delta. | ![[Maple Plot]](images/spojitost23.gif)
Funkce y=exp(x) není Lipschitzovská. Delta klesá rychle k nule. | ![[Maple Plot]](images/spojitost32.gif)
Funkce y=x2 není Lipschitzovská. Delta klesá docela rychle k nule. | ![[Maple Plot]](images/spojitost36.gif)
Funkce | ![[Maple Plot]](images/spojitost42.gif)
Funkce y=sin(x) zobrazená na intervalu <-Pi/2,Pi/2> je Liptchitzovská. Delta se nikdy neblíží k nule. |
|
Vlevo je červený graf funkce, žluté jsou fixní epsilon na ose y a měnící se delta na ose x. V pravo modrý graf znázorňuje velikost delta při fixním epsilon . Velikost delta se mění v závislosti na průchodu červeným grafem funkce podlél osy y (podle polohy epsilon v grafu). |
||||
![[Maple Plot]](images/spojitost60.gif) |
![[Maple Plot]](images/spojitost24.gif) |
![[Maple Plot]](images/spojitost33.gif) |
![[Maple Plot]](images/spojitost39.gif) |
![[Maple Plot]](images/spojitost43.gif) |
Pokud je modrý graf klesající, tak funkce není Lipschitzovská, protože nelze najít konstantu L , která by splňovala Lipschitzovskou podmínku pro všechna x.
Lipschitzovská podmínka:
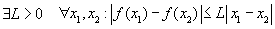
Položíme-li
![]() a
a
![]() dostaneme
dostaneme
![]() nebo-li
nebo-li
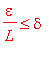
Takže pokud se nám delta neustále zmenšuje až k nule, tak pro dané epsilon neexistuje Lipchitzovská konstanta L .
Pokud delta klesá k nule ve směru osy kde je znázorněno f(x) (tedy y), tak funkce není Lipschitzovská.
Pokud je delta ostře větší než nula
i pro libovolně malé
epsilon
ostře větší než nula a
delta
je konstantní nebo roste, tak existuje konstanta
L
a funkce je Lipschitzovská.
Monotonie
delta
lze určit pomocí první derivace funkce. Pokdu je absolutní hodnota první derivace rostoupcí, tak
delta
se zmenšuje, protože funkce roste stále rychleji nahorů nebo dolů.
Pokud je absolutní hodnota první derivace konstantní nebo klesající, tak je
delta
konstantí nebo se zvětšuje, protože funkce se stále "zpomaluje" (stále pomaleji klesá nebo roste).
![]()
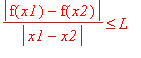
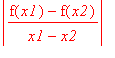
![]()
![]()
![]()
Lipschitzovská konstanta L se dá určit pomocí prvních derivací, a to tak, že najdeme maximum |f'(x)| přes všechna x . Na derivaci lez pohlížet jako na směrnici, stejně jako na konstantu L , tedy můžeme za L dosadit jakoukoliv konstantu větší než absolutní hodnota první derivace funkce f(x) .
|
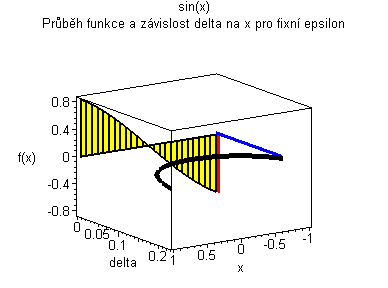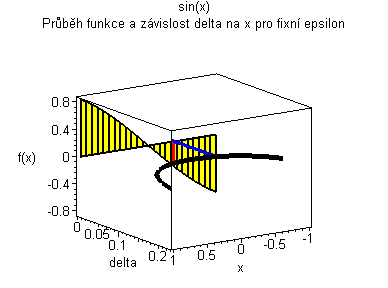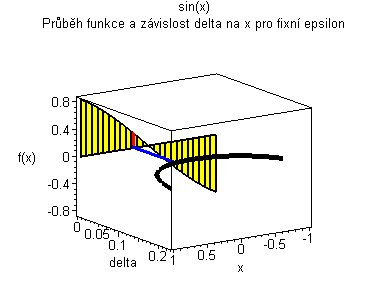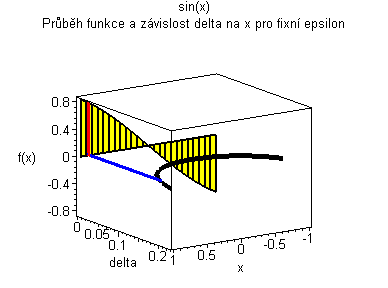
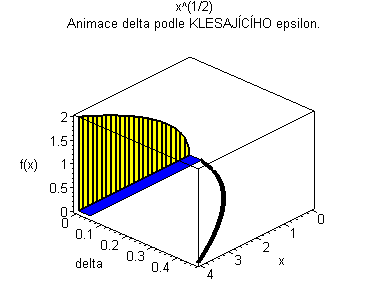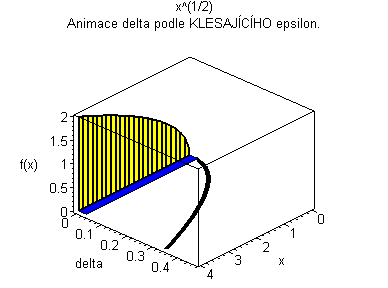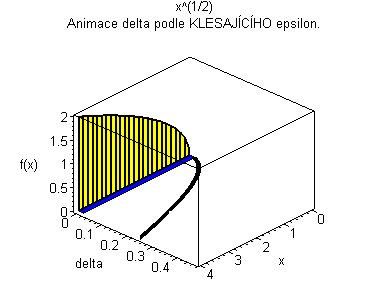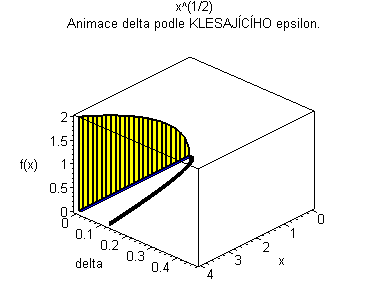
Trojrozměrná animace |
|
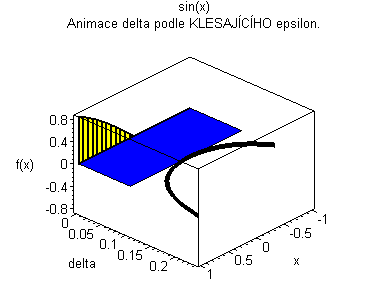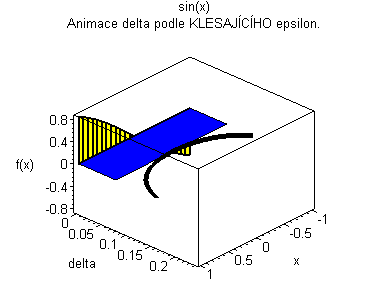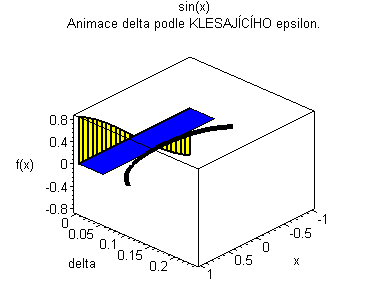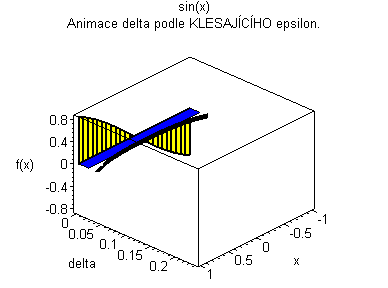
| Žlutý graf znázorňuje průběh funkce. Modrá značka ukazuje měnící se delta v závislosti na x pro fixní epsilon. | Černý graf je animace delta přes klesající epsilon. Modrý obdélníček znázorňuje minimální delta pro dané epsilon. |
 |
 |
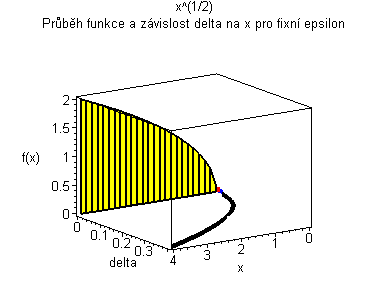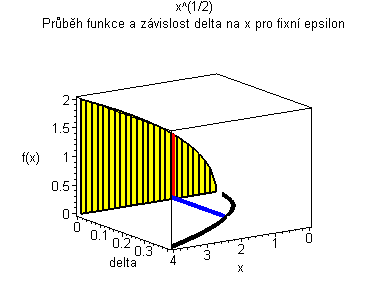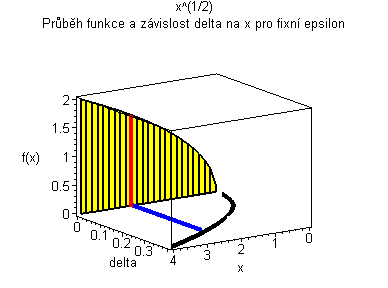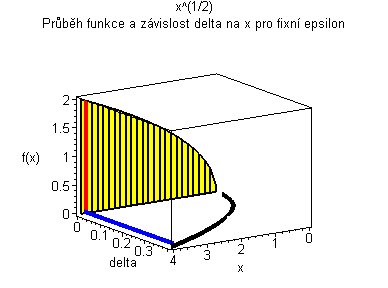 |
 |
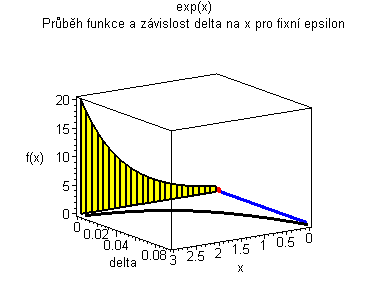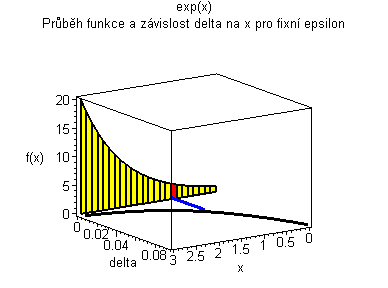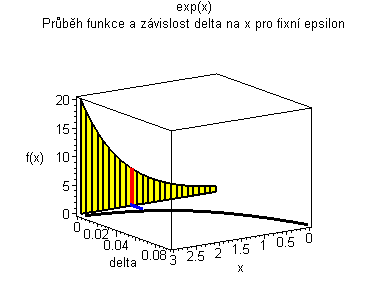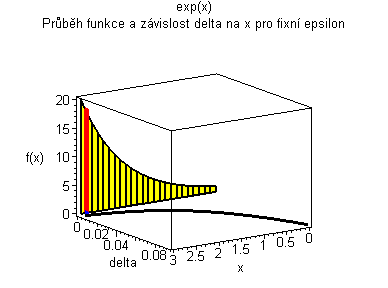 |
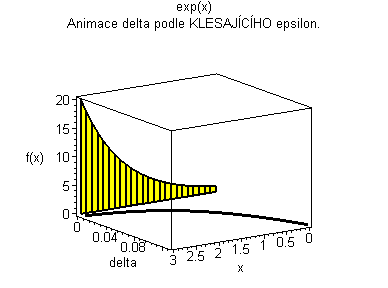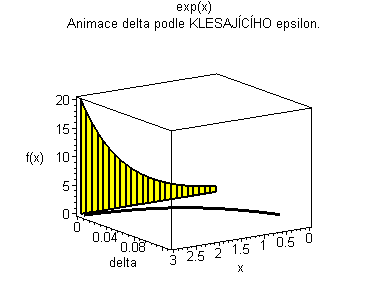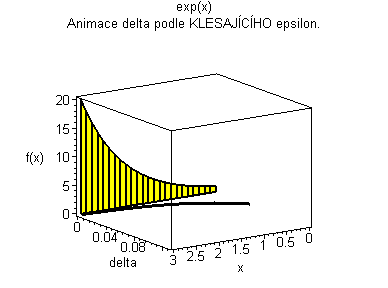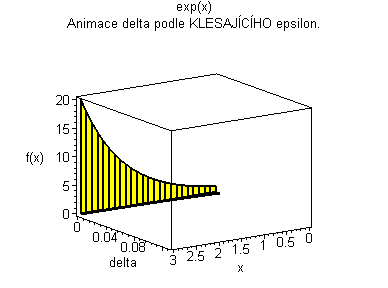 |
Derivace součinu funkcí
Nechť funkce s je spojitá v bodě x. Její derivaci v bodě x lze vyjádřit jako:
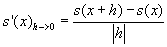
Derivace součinu funkcí f a g v bodě x, lze vyjádřit jako:
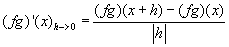
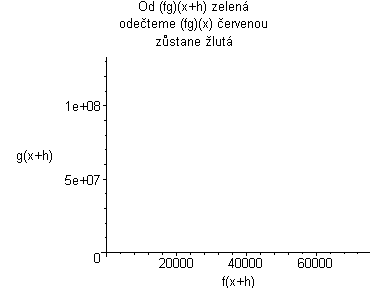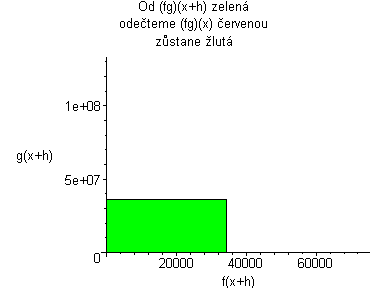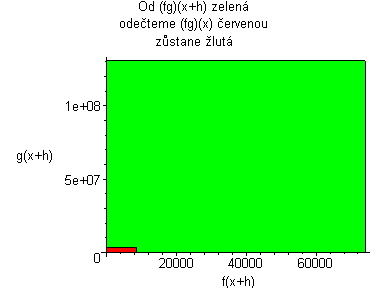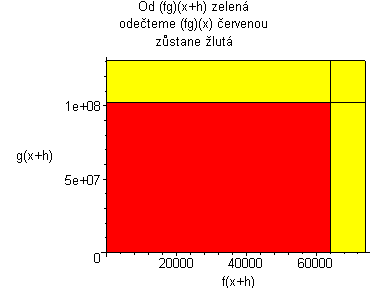
|
Kde: zelená plocha znázorňuje (fg)(x+h) červená plocha znázorňuje (fg)(x) Když červenou odečteme od zelené, tak zůstane žlutá plocha. žlutá:= f(x)(g(x+h)-g(x))+g(x)(f(x+h)-f(x))+((f(x+h)-f(x))(g(x+h)-g(x))) Když dosadíme do vzorce, tak žlutá plocha lze vyjádřit jako: 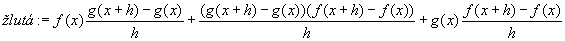
|
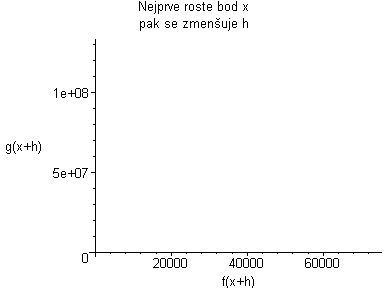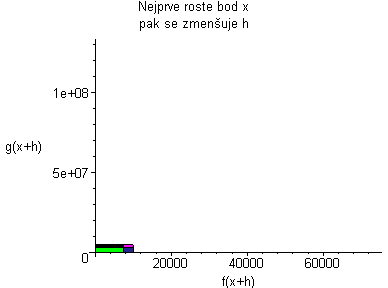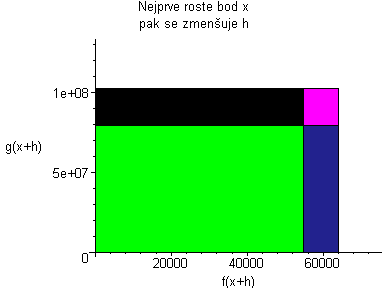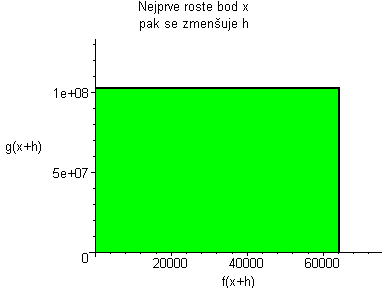
|
Plochu (fg)(x+h) animujeme podle rostoucího x, a pak se díváme co se děje s grafem, když h se blíží k nule. Po dosazení do vzorce dostaneme vztahy: 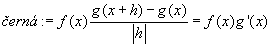 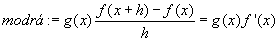 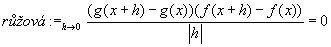 Pro h jdoucí k nule dostaneme tedy vzorec pro derivaci součinu: 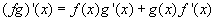
|
 |
 |
 |
 |
| Pro zajímavost: Součin funcí a derivace Srovnání grafů Součinu derivací a Derivace součinu. |
|
![[Maple Plot]](images/spojitost53.gif) |
![[Maple Plot]](images/spojitost57.gif) |
![[Maple Plot]](images/spojitost56.gif) |
![[Maple Plot]](images/spojitost58.gif) |
![[Maple Plot]](images/spojitost55.gif) |
![[Maple Plot]](images/spojitost61.gif) |