



Next: Compactifications of the real
Up: Irreducible circle-like continua
Previous: Irreducible circle-like continua
A
solenoid
is a continuum homeomorphic to
the inverse limit
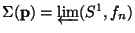 of the inverse sequence of unit circles
of the inverse sequence of unit circles  in the complex
plane with bonding maps
in the complex
plane with bonding maps
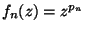 , where
, where
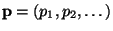 is a sequence of prime numbers; it is
called a
is a sequence of prime numbers; it is
called a
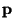 -adic solenoid
. The solenoid
-adic solenoid
. The solenoid
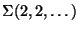 is known as a
dyadic solenoid
.
is known as a
dyadic solenoid
.
Geometrically, solenoid
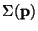 can be described
as the intersection of a sequence of solid tori
can be described
as the intersection of a sequence of solid tori
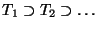 such that
such that 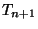 wraps
wraps 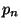 times around
times around 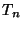 without
folding and
without
folding and 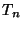 is
is
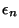 -thin, for each
-thin, for each
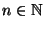 , where
, where
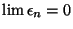 .
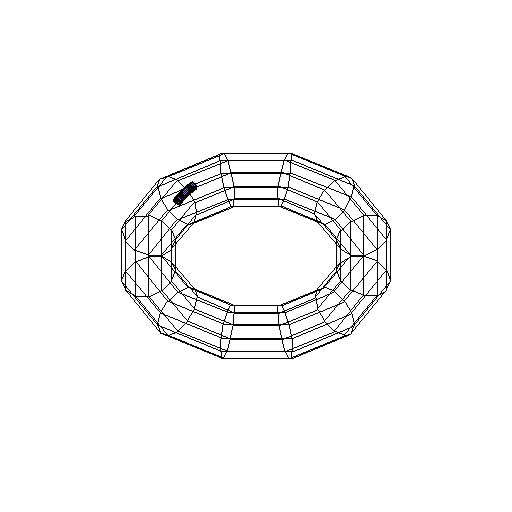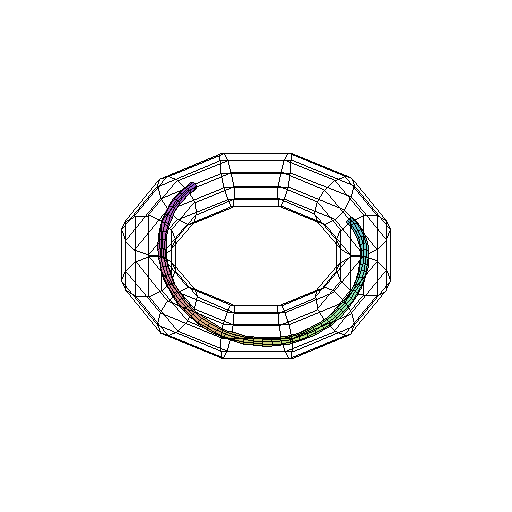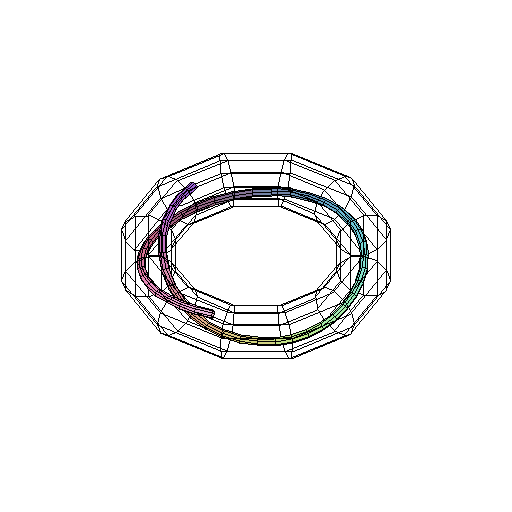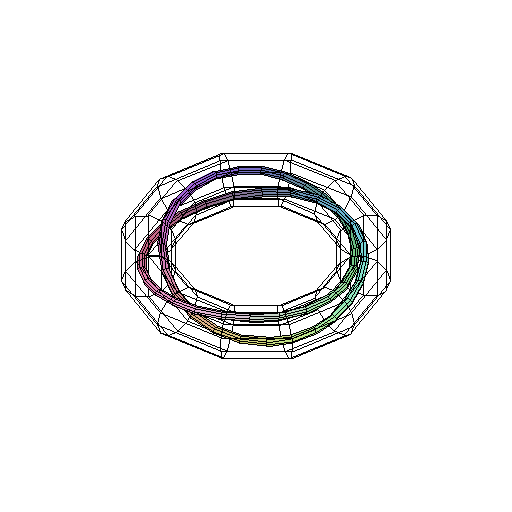
See Figure A.
.
See Figure A.
Figure 4.3.1:
( A ) dyadic selenoid
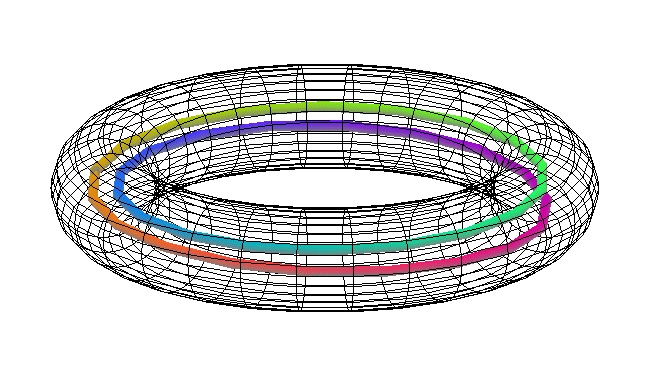 |
Figure:
( AA ) dyadic selenoid - an animation
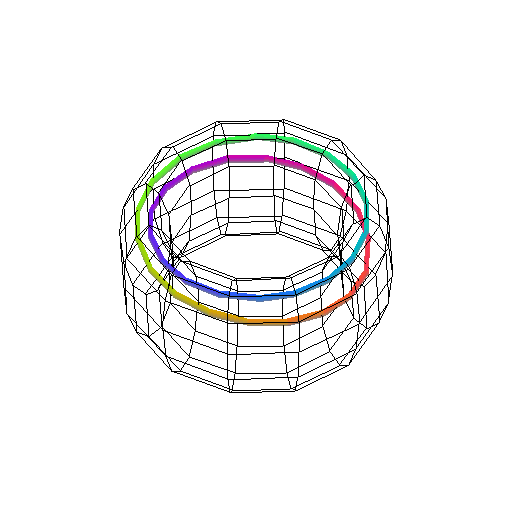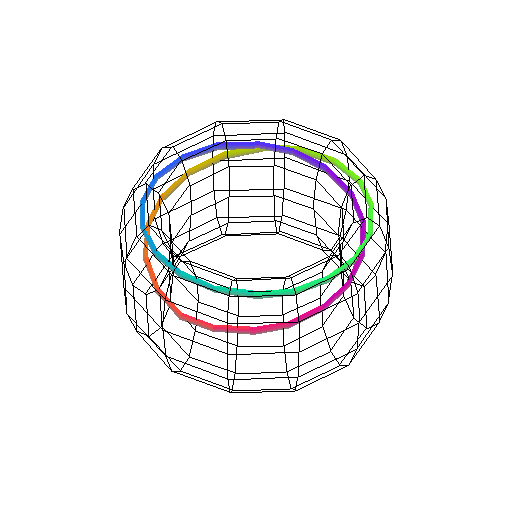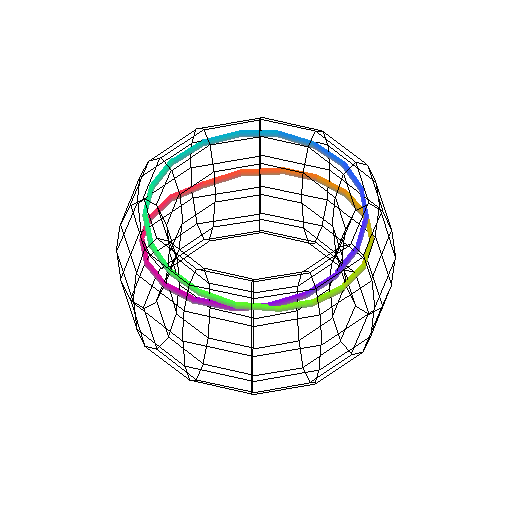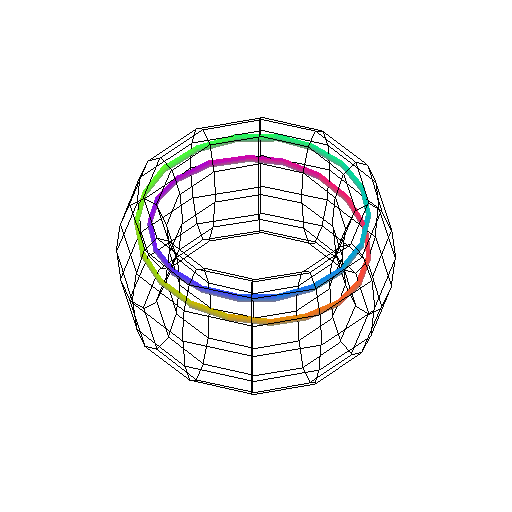 |
Figure:
( AAA ) dyadic selenoid - an animation with a knot ;-)
 |
- Each solenoid can be constructed (up to a homeomorphism)
as the quotient space of the product
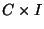 by identifying
each point
by identifying
each point 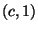 with
with 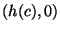 , where
, where 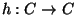 is
a homeomorphism of the Cantor set
is
a homeomorphism of the Cantor set 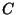 such that
for every
such that
for every
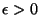 there exist a closed-open subset
there exist a closed-open subset 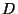 of
of 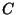 and a positive integer
and a positive integer 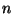 such that
such that
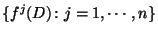 is a cover of
is a cover of 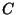 consisting of
pairwise disjoint subsets of
consisting of
pairwise disjoint subsets of 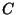 with diameters less than
with diameters less than
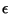 [Gutek 1980].
[Gutek 1980].
- Each solenoid
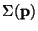 is an Abelian
topological group with a group operation
is an Abelian
topological group with a group operation
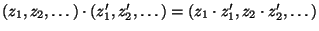 and the neutral element
and the neutral element
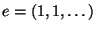 .
.
- Either of the following conditions is equivalent for a
nondegenerate continuum
 different from
a simple closed curve to be a solenoid.
different from
a simple closed curve to be a solenoid.
 is homeomorhic to a one-dimensional
topological group [Hewitt 1963];
is homeomorhic to a one-dimensional
topological group [Hewitt 1963];
 is indecomposable and is homeomorphic to a topological group
[Chigogidze 1996, Theorem 8.6.18];
is indecomposable and is homeomorphic to a topological group
[Chigogidze 1996, Theorem 8.6.18];
 is circle-like, has the
property of Kelley and contains no
local end point [Krupski 1984c, Theorem (4.3)];
is circle-like, has the
property of Kelley and contains no
local end point [Krupski 1984c, Theorem (4.3)];
 is circle-like, has the property of Kelley, each proper
nondegenerate subcontinuum of
is circle-like, has the property of Kelley, each proper
nondegenerate subcontinuum of  is an arc and
is an arc and  has no
end pointsend point;
has no
end pointsend point;
 is circle-like, has the property of Kelley and has an
open cover by Cantor bundles of open arcs (i.e., sets homeomorphic
to the product
is circle-like, has the property of Kelley and has an
open cover by Cantor bundles of open arcs (i.e., sets homeomorphic
to the product
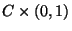 of the Cantor set
of the Cantor set 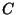 and the
open interval
and the
open interval 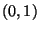 ) [Krupski 1982];
) [Krupski 1982];
 is homogeneous, contains no proper,
nondegenerate, terminal subcontinua
and sufficiently small subcontinua of
is homogeneous, contains no proper,
nondegenerate, terminal subcontinua
and sufficiently small subcontinua of  are not
are not
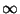 -ods [Krupski 1995, Theorem
3.1];
-ods [Krupski 1995, Theorem
3.1];
 is a homogeneous curve containing an open subset
is a homogeneous curve containing an open subset 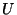 such that some component of
such that some component of 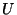 does not have the
disjoint arcs property [Krupski 1995, p.
166];
does not have the
disjoint arcs property [Krupski 1995, p.
166];
 is a homogeneous finitely cyclic (or, equivalently,
is a homogeneous finitely cyclic (or, equivalently, 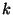 -junctioned) curve that is not tree-like and contains no
nondegenerate, proper, terminal subcontinua
[Krupski et al. XXXXb], [Duda et al. 1991].
-junctioned) curve that is not tree-like and contains no
nondegenerate, proper, terminal subcontinua
[Krupski et al. XXXXb], [Duda et al. 1991].
 is openly homogeneous and
sufficiently small subcontinua of
is openly homogeneous and
sufficiently small subcontinua of  are arcs
[Prajs 1989];
are arcs
[Prajs 1989];
- Solenoid
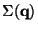 is a continuous image of
is a continuous image of
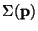 if and only if the sequence
if and only if the sequence
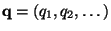 is a
factorant of sequence
is a
factorant of sequence
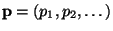 , i.e.,
there exists
, i.e.,
there exists 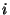 such that for each
such that for each 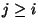 there is
there is 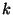 such
that
such
that
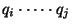 is a factor of
is a factor of
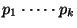 .
.
Two solenoids are homeomorphic if and only if each of them is a
continuous image of another
[Cook 1967], [D. van Dantzig 1930, Satz 8, p. 122].
There is a family of solenoids of cardinality
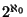 such that no member of the family is a continuous image of another.
such that no member of the family is a continuous image of another.
- Each monotonemonotone map image of a solenoid
 is
homeomorphic to
is
homeomorphic to  [Krupski 1984b, Theorem 5].
[Krupski 1984b, Theorem 5].
Each open map transforms  onto a solenoid or onto
an arc-like continuum with the property of Kelley and with arcs
as proper nondegenerate subcontinua; if the map is a local homeomorphism,
then its image is a solenoid [Krupski 1984a].
onto a solenoid or onto
an arc-like continuum with the property of Kelley and with arcs
as proper nondegenerate subcontinua; if the map is a local homeomorphism,
then its image is a solenoid [Krupski 1984a].
- The composant of a solenoid
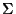 containing
containing  is a one-parameter
topological subgroup of
is a one-parameter
topological subgroup of 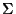 , i.e. it is a one-to-one continuous
homomorphic image of the additive group of the reals.
, i.e. it is a one-to-one continuous
homomorphic image of the additive group of the reals.
- Any two composants of any two solenoids are
homeomorphic [R. de Man 1995].
- No solenoid can be mapped onto a strongly self-entwined continuum. In
particular, it cannot be mapped onto a circle-like plane
continuum which is a common part of a descending sequence of
circular chains
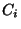 such that
such that 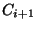 circles
circles 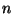 times
in
times
in 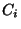 clockwisely and then
clockwisely and then 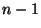 times
counter-clockwisely and the first link of
times
counter-clockwisely and the first link of 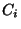 contains the
closure of the first link of
contains the
closure of the first link of 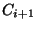 [Rogers 1971b].
[Rogers 1971b].
- No movable continuum (in particular no
continuum lying in a surface or a tree-like continuum) can be continuously mapped onto a
solenoid. Alternatively, if the first Alexander-Cech
cohomology group of a continuum
 is finitely
divisiblefinitely divisible group, then
is finitely
divisiblefinitely divisible group, then  cannot be
mapped onto a solenoid [Krasinkiewicz 1976, Remark, p. 46, 4.1, 4.9.,
5.1], [Krasinkiewicz 1978, Corollary
7.3], [Rogers 1975].
cannot be
mapped onto a solenoid [Krasinkiewicz 1976, Remark, p. 46, 4.1, 4.9.,
5.1], [Krasinkiewicz 1978, Corollary
7.3], [Rogers 1975].
- Every nonplanar, circle-like continuum has the
shape of a solenoid [Krasinkiewicz 1976, remark, p.
46]. Two solenoids have the same shape
if and only if they are homeomorphic
[Godlewski 1970].
- Any autohomeomorphism
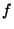 of
of
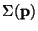 is isotopic
to a homeomorphism
is isotopic
to a homeomorphism 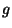 which is induced by a map
which is induced by a map
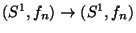 of the inverse sequences which
define
of the inverse sequences which
define
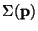 (
(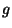 can be a group translation,
the involution, a power map or its inverse, or compositions
of these maps). Maps
can be a group translation,
the involution, a power map or its inverse, or compositions
of these maps). Maps 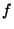 and
and 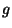 have equal the topological
entropies and are
semi-conjugate if the entropy is positive
[Kwapisz 2001, Theorems 1-3, pp. 252-253], [D. van Dantzig 1930, Satz
9, p. 125].
have equal the topological
entropies and are
semi-conjugate if the entropy is positive
[Kwapisz 2001, Theorems 1-3, pp. 252-253], [D. van Dantzig 1930, Satz
9, p. 125].
The topological group of all autohomeomorphisms
(with the compact-open topology) of a solenoid 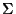 is homeomorphic (but not isomorphic)
to the the product
is homeomorphic (but not isomorphic)
to the the product
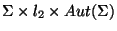 ,
where
,
where 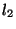 is the Hilbert space and the group
is the Hilbert space and the group
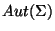 of all topological group automorphisms of
of all topological group automorphisms of 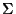 is equipped with
the discrete topology and it is equal to
is equipped with
the discrete topology and it is equal to
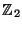 ,
or
,
or
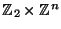 ,
or
,
or
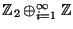 [Keesling 1972, Theorems 3.1 and 2.4].
[Keesling 1972, Theorems 3.1 and 2.4].
- If the spaces of all autohomeomorphisms of two solenoids are homeomorphic,
then the solenoids are isomorphic as topological groups
[Keesling 1972, Corollary 3.9].
- Any map
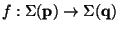 is,
for every
is,
for every
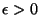 ,
, 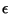 -homotopic to a map
induced by a map
-homotopic to a map
induced by a map
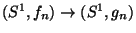 between inverse sequences
defining the corresponding solenoids [Rogers et al. 1971].
between inverse sequences
defining the corresponding solenoids [Rogers et al. 1971].
- A
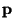 -adic solenoid admits a mean if and
only if infinitely many numbers in the sequence
-adic solenoid admits a mean if and
only if infinitely many numbers in the sequence 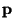 equal 2 [Krupski XXXXa]. The same condition is
equivalent to the non-existence of exactly 2-to-1 map
defined on the solenoid [Debski 1992].
equal 2 [Krupski XXXXa]. The same condition is
equivalent to the non-existence of exactly 2-to-1 map
defined on the solenoid [Debski 1992].
- The hyperspace of all subcontinua of any
solenoid
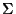 is homeomorphic the cone over
is homeomorphic the cone over 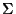 [Rogers 1971a], [Nadler 1991, p. 202].
[Rogers 1971a], [Nadler 1991, p. 202].
- The family of all solenoids in the cube
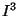 (as a subset of the hyperspace
(as a subset of the hyperspace 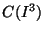 ) is Borel
and not
) is Borel
and not
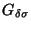 [Krupski XXXXc].
[Krupski XXXXc].
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.




Next: Compactifications of the real
Up: Irreducible circle-like continua
Previous: Irreducible circle-like continua
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() of the inverse sequence of unit circles
of the inverse sequence of unit circles ![]() in the complex
plane with bonding maps
in the complex
plane with bonding maps
![]() , where
, where
![]() is a sequence of prime numbers; it is
called a
is a sequence of prime numbers; it is
called a
![]() -adic solenoid
. The solenoid
-adic solenoid
. The solenoid
![]() is known as a
dyadic solenoid
.
is known as a
dyadic solenoid
.
![]() can be described
as the intersection of a sequence of solid tori
can be described
as the intersection of a sequence of solid tori
![]() such that
such that ![]() wraps
wraps ![]() times around
times around ![]() without
folding and
without
folding and ![]() is
is
![]() -thin, for each
-thin, for each
![]() , where
, where
![]() .
See Figure A.
.
See Figure A.
![]() such that no member of the family is a continuous image of another.
such that no member of the family is a continuous image of another.
![]() onto a solenoid or onto
an arc-like continuum with the property of Kelley and with arcs
as proper nondegenerate subcontinua; if the map is a local homeomorphism,
then its image is a solenoid [Krupski 1984a].
onto a solenoid or onto
an arc-like continuum with the property of Kelley and with arcs
as proper nondegenerate subcontinua; if the map is a local homeomorphism,
then its image is a solenoid [Krupski 1984a].
![]() is homeomorphic (but not isomorphic)
to the the product
is homeomorphic (but not isomorphic)
to the the product
![]() ,
where
,
where ![]() is the Hilbert space and the group
is the Hilbert space and the group
![]() of all topological group automorphisms of
of all topological group automorphisms of ![]() is equipped with
the discrete topology and it is equal to
is equipped with
the discrete topology and it is equal to
![]() ,
or
,
or
![]() ,
or
,
or
![]() [Keesling 1972, Theorems 3.1 and 2.4].
[Keesling 1972, Theorems 3.1 and 2.4].