



Next: Universal dendrites of order
Up: Dendrites
Previous: Universal dendrites
By the
Wazewski universal dendrite
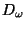 we mean a dendrite
we mean a dendrite 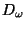 such that
each ramification point of
such that
each ramification point of 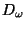 is of order
is of order 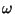 and for each arc
and for each arc
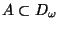 the set of ramification points of
the set of ramification points of
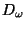 which belong to
which belong to 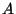 is dense in
is dense in 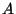 . Its
construction, known from [Whyburn 1942, Chapter K, p.
137] (compare also [Menger 1932, Chapter X, Section 6,
p. 318]), is the following.
. Its
construction, known from [Whyburn 1942, Chapter K, p.
137] (compare also [Menger 1932, Chapter X, Section 6,
p. 318]), is the following.
Let
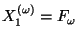 . At the midpoint
. At the midpoint 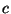 of each
maximal free arc contained in
of each
maximal free arc contained in
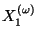 (obviously the arc is a straight line segment) attach a
sufficiently small copy of
(obviously the arc is a straight line segment) attach a
sufficiently small copy of 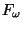 so that
so that 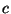 is the
only common point of
is the
only common point of
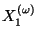 and of the attached
copy. Denote by
and of the attached
copy. Denote by
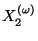 the union of
the union of
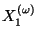 and of all attached copies. Thus
and of all attached copies. Thus
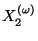 is a dendrite. At the midpoint of each
maximal free arc contained in
is a dendrite. At the midpoint of each
maximal free arc contained in
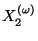 we perform
the same construction, i.e., we attach a sufficiently small
copy of
we perform
the same construction, i.e., we attach a sufficiently small
copy of 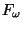 so that
so that 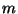 is the only common point of
is the only common point of
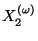 and of the attached copy. Denote by
and of the attached copy. Denote by
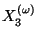 the union of
the union of
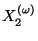 and of all
attached copies. Thus
and of all
attached copies. Thus
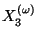 is a dendrite.
Continuing in this way we obtain an increasing sequence of
dendrites
is a dendrite.
Continuing in this way we obtain an increasing sequence of
dendrites
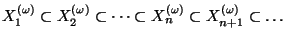 . The construction can be done in the plane
in such a way that the limit continuum
. The construction can be done in the plane
in such a way that the limit continuum 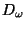 defined by
defined by
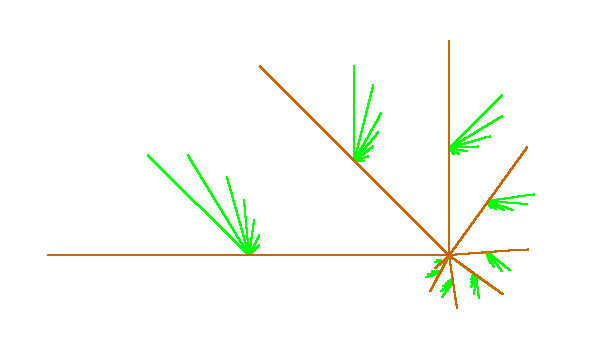
is again a dendrite. See Figure A.
Figure 1.3.6:
( A ) Wazewski universal dendrite 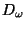
 |
For another construction of 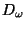 (using inverse limits) see
[Nadler 1992, 10.37, p. 181-185].
(using inverse limits) see
[Nadler 1992, 10.37, p. 181-185].
The following properties of 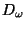 are known.
are known.
 is universal in the class of all
dendrites (see e.g. [Nadler 1992, 10.37, p. 181-185]).
is universal in the class of all
dendrites (see e.g. [Nadler 1992, 10.37, p. 181-185]).
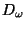 is embeddable in the plane (in fact, it is constructed in
the plane).
is embeddable in the plane (in fact, it is constructed in
the plane).
- Each open image of
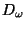 is homeomorphic to
is homeomorphic to
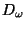 (see [Chaaratonik 1980, Theorem 1, p. 490]).
(see [Chaaratonik 1980, Theorem 1, p. 490]).
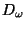 is homogeneous with respect to monotone mappings,
[Charatonik 1991, Theorem 7.1, p. 186].
is homogeneous with respect to monotone mappings,
[Charatonik 1991, Theorem 7.1, p. 186].
For other mapping properties of 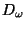 , in particular ones related to
the action of the group of autohomeomorphisms on
, in particular ones related to
the action of the group of autohomeomorphisms on 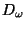 ,
see [Charatonik 1995].
,
see [Charatonik 1995].
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.




Next: Universal dendrites of order
Up: Dendrites
Previous: Universal dendrites
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
![]() . At the midpoint
. At the midpoint ![]() of each
maximal free arc contained in
of each
maximal free arc contained in
![]() (obviously the arc is a straight line segment) attach a
sufficiently small copy of
(obviously the arc is a straight line segment) attach a
sufficiently small copy of ![]() so that
so that ![]() is the
only common point of
is the
only common point of
![]() and of the attached
copy. Denote by
and of the attached
copy. Denote by
![]() the union of
the union of
![]() and of all attached copies. Thus
and of all attached copies. Thus
![]() is a dendrite. At the midpoint of each
maximal free arc contained in
is a dendrite. At the midpoint of each
maximal free arc contained in
![]() we perform
the same construction, i.e., we attach a sufficiently small
copy of
we perform
the same construction, i.e., we attach a sufficiently small
copy of ![]() so that
so that ![]() is the only common point of
is the only common point of
![]() and of the attached copy. Denote by
and of the attached copy. Denote by
![]() the union of
the union of
![]() and of all
attached copies. Thus
and of all
attached copies. Thus
![]() is a dendrite.
Continuing in this way we obtain an increasing sequence of
dendrites
is a dendrite.
Continuing in this way we obtain an increasing sequence of
dendrites
![]() . The construction can be done in the plane
in such a way that the limit continuum
. The construction can be done in the plane
in such a way that the limit continuum ![]() defined by
defined by
![]() (using inverse limits) see
[Nadler 1992, 10.37, p. 181-185].
(using inverse limits) see
[Nadler 1992, 10.37, p. 181-185].
![]() are known.
are known.
![]() , in particular ones related to
the action of the group of autohomeomorphisms on
, in particular ones related to
the action of the group of autohomeomorphisms on ![]() ,
see [Charatonik 1995].
,
see [Charatonik 1995].