



Next: indecomposable
Up: Definitions
Previous: HU-terminal
Given a continuum X with a metric d, we let 2X to denote the
hyperspace of all nonempty closed subsets of X equipped with the
Hausdorff metric H defined by
(see e.g. [64, (0.1), p. 1 and (0.12), p. 10]).
If H(A, An) tends
to zero as n tends to infinity, we put
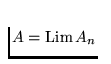 . Further, we denote
by F1(X) the hyperspace of singletons of X, and by C(X) the hyperspace of all
subcontinua of X, i.e., of all connected elements of 2X. Since X is
homeomorphic to F1(X), there is a natural embedding of X into C(X),
and so we can write
. Further, we denote
by F1(X) the hyperspace of singletons of X, and by C(X) the hyperspace of all
subcontinua of X, i.e., of all connected elements of 2X. Since X is
homeomorphic to F1(X), there is a natural embedding of X into C(X),
and so we can write
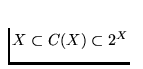 . Thus one can consider a
retraction from either C(X) or 2X onto X.
. Thus one can consider a
retraction from either C(X) or 2X onto X.
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21
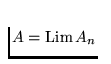 . Further, we denote
by F1(X) the hyperspace of singletons of X, and by C(X) the hyperspace of all
subcontinua of X, i.e., of all connected elements of 2X. Since X is
homeomorphic to F1(X), there is a natural embedding of X into C(X),
and so we can write
. Further, we denote
by F1(X) the hyperspace of singletons of X, and by C(X) the hyperspace of all
subcontinua of X, i.e., of all connected elements of 2X. Since X is
homeomorphic to F1(X), there is a natural embedding of X into C(X),
and so we can write
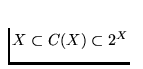 . Thus one can consider a
retraction from either C(X) or 2X onto X.
. Thus one can consider a
retraction from either C(X) or 2X onto X.