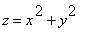 . Tato rovnice odpovídá speciálnímu a to kruhovému neboli rotačnímu paraboloidu a eliptický
. Tato rovnice odpovídá speciálnímu a to kruhovému neboli rotačnímu paraboloidu a eliptický
Paraboloidy
Paraboloidy, jakožto kvadriky, jsou z hlediska afinní klasifikace dva. Eliptický a hyperbolický.
I . Eliptický paraboloid
V kanonické bázi má vyjádření
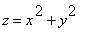 . Tato rovnice odpovídá speciálnímu a to kruhovému neboli rotačnímu paraboloidu a eliptický
. Tato rovnice odpovídá speciálnímu a to kruhovému neboli rotačnímu paraboloidu a eliptický
z něho snadno dostaneme afinitou.
Plocha je to neomezená a proto si ji pro naše účely omezíme podmínkou
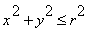 . tj. budeme uvažovat pouze jeho část od vrcholu
. tj. budeme uvažovat pouze jeho část od vrcholu
až po rovnoběžkovou kružnici s poloměrem r .
Jeho parametrické vyjádření je např. takovéto
![p(u,v) = [u, v, u^2+v^2]](images/plochy-paraboloidy3.gif) .
.
Nyní si spočteme povrch námi uvažovné části ( obsah "horního" kruhu do povrchu nepočítáme ). K tomu spočteme parciální derivace jeho porametrizace
a následovně první formu plochy.
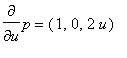
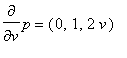 a tedy
a tedy

![]()
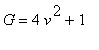
Povrch plochy spočteme takto: ( EDIT -EXECUTE - WORKSHEET )
| > | S=Int(Int(sqrt(E*G-F^2),u=a..b),v=c..d); |
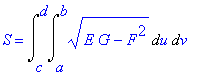
Po dosazení tedy máme spočíst dvojný integrál z integrandu
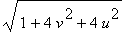 s podmínkou
s podmínkou
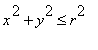 .
.
Výpočet si usnadníme substitucí do polárních souřadnic
![]()
![]() je z intervalu
je z intervalu
![]()
![]()
![]() je z intervalu
je z intervalu
![]() . Jakobián je roven
. Jakobián je roven
![]() .
.
Dostáváme tedy:
| > | S=Int(Int(s*sqrt(1+4*s^2),s=0..r),f=0..2*Pi); |
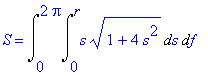
což snadno dopočteme pomocí substituce
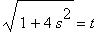 .
.
| > | 1/4*2*Pi*Int(t^2,t=1..sqrt(1+4*r^2))=Pi/6*((1+4*r^2)*sqrt(1+4*r^2)-1); |
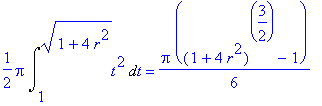
Máme tedy povrch časti rotačního paraboloidu
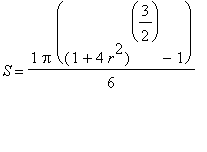 .
.
Ještě si tuto plochu nakreslíme:
| > | r:=1: |
| > | plot3d(x^2+y^2,x=-r..r,y=-sqrt(r^2-x^2)..sqrt(r^2-x^2)); |
![[Maple Plot]](images/plochy-paraboloidy23.gif)
II . Hyperbolický paraboloid
V kanonické bázi má rovnici
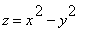 . Pro tuto plochu spočteme to, co jsme udělali pro paraboloid eliptický.
. Pro tuto plochu spočteme to, co jsme udělali pro paraboloid eliptický.
Parametrické vyjadření je :
![p(u,v) = [u, v, u^2-v^2]](images/plochy-paraboloidy25.gif) .
.
Dále
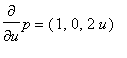
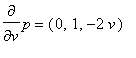 a tedy
a tedy
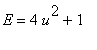
![]()
 .
.
První forma se u obou ploch sice liší o znamení u složky
![]() , ale výraz
, ale výraz
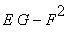 zůstává stejný. Proto při výpočtu povrchu plochy, kterou bychom
zůstává stejný. Proto při výpočtu povrchu plochy, kterou bychom
omezili jako v předchozím případě, dostáváme stejný výsledek.
Na obou plochách se tedy "měří" stejně.
Ještě zbývá obrázek: ( plocha je opět zobrazena nad kruhovým půdorysem )
| > | plot3d(x^2-y^2,x=-r..r,y=-sqrt(r^2-x^2)..sqrt(r^2-x^2),orientation=[-60,72]); |
![[Maple Plot]](images/plochy-paraboloidy33.gif)
| > |