Kisoida
Kisoida je rovinná křivka, kterou odvodíme pomocí kružnice se středem v počátku a s poloměrem r .
Kružnice má parametrizaci:
![]()
Spočteme tečný vektor:
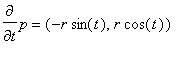
Hledanou křivku si označíme
![]() a budeme ji hledat jako křivku, jejiž body leží na tečnách ke kružnici a zároveň tak, aby byla kolmá na systém
a budeme ji hledat jako křivku, jejiž body leží na tečnách ke kružnici a zároveň tak, aby byla kolmá na systém
tečen kružnice.
Musí tedy platit
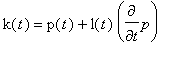 .
.
Budme nyní hledat vyjádření funkce
![]() tak, aby tečný vektor křivky
tak, aby tečný vektor křivky
![]() byl kolmý na tečný
byl kolmý na tečný
vektor kružnice. Nejprve spočteme tečný vektor křivky
![]() .
.
{ spuštění ........ EDIT - WORKSHEET - EXECUTE )
| > | restart: |
| > | with(plots): |
| > | k(t):= p(t)+l(t)*Diff(p(t),t): |
| > | Diff(k,t)=diff(k(t),t); |
| > |
![]()
| > |
Aby jsme dosáhli kolmosti, tak tuto rovnici vynásobíme skalárně
![]() a položíme rovno nule, tedy
a položíme rovno nule, tedy
| > | 0=(1+Diff(l,t))*Diff(p,t)*Diff(p,t)+l(t)*Diff(p,t,t)*Diff(p,t); |
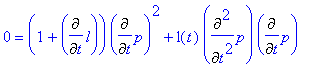
Snadno spočteme, že
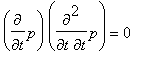 a
a
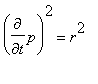
Dosazením dostáváme rovnici, kterou snadno vyřešíme ( aditivní konstanta je rovna nule )
| > | Diff(l(t),t)=-1; |
![]()
| > | l(t)=-t; |
![]()
Můžeme tedy napsat rovnici kisoidy:
![]() .
.
Ještě si povšimneme vzdálenosti bodů
![]() a
a
![]() . Je totiž rovna
. Je totiž rovna
![]() , což je právě délka oblouku kružnice příslušná parametru
t
.
, což je právě délka oblouku kružnice příslušná parametru
t
.
Proto se také kisoida nazývá též odvynovka, protože ji lze získat také prakticky takto. Například na kruh (válec) namotáme provázek upevněný
v jednom bodě k povrchu a potom konec provázku při odvíjení ( musí být stále napnutý ) opisuje právě kisoidu.
Nyní si tuto křivku nakreslíme.
| > | r:=1: |
| > | A:=plot([r*cos(t)+t*r*sin(t), r*sin(t)-t*r*cos(t),t=0..2*Pi]): |
| > | B:=plot([r*cos(t),r*sin(t),t=0..2*Pi],color=green): |
| > | display({A,B},scaling=constrained); |
![[Maple Plot]](images/krivka-kisoida19.gif)
Pro názornost vzniku kisoidy si ji vytvoříme ještě následující animací.
| > | C:=animate([r*cos(t)-tt*r*sin(t),r*sin(t)+tt*r*cos(t),tt=0..0.1],t=0..2*Pi,color=black): |
| > | E:=animate([r*cos(t),r*sin(t),t=0..2*Pi],tt=0..1,color=green): |
| > | bod:=animate([r*cos(t*s)+s*t*r*sin(t*s),r*sin(t*s)-s*t*r*cos(t*s),s=0..1],t=0..2*Pi,color=red): |
| > | F:=animate([r*cos(t)+tt*(r*cos(t)-r*cos(t)+t*r*sin(t)),r*sin(t)+tt*(r*sin(t)-r*sin(t)-t*r*cos(t)),tt=0..1],t=0..2*Pi,color=blue): |
| > | display(C,E,F,bod,scaling=constrained); |
![[Maple Plot]](images/krivka-kisoida20.gif)
| > |
Animaci lze spustit kliknutím na obrázek a poté na ikonku PLAY na horní liště
Délka modré úsečky je právě délka oblouku kružnice od bodu [r,0] do bodu dotyku tečny. Po animaci je tedy rovna
![]() .
.