Matematika na PC - Maple V Release 5

PŘEPNOUT: včetně Maple textu

MAPLE - LAPLACEOVA TRANSFORMACE

Příklady jsou zpracované v Maple V Release 5
zdroj je možné stáhnou zde - muklap.zip -

Lapalceova transformace

Definice

je dána funkce f z <0, ) --> R

F(s) je Laplaceova transformace, pokud existuje pro dostatečně velká s

F(s) je definována jako:

Příklad funkce f(t) a její Laplaceovy transformace F(s)

V grafu je ukázaná funkce f = exp(at) jak roste v závislosti na parametru a a její Laplaceova transformace F=1/(s-a) v závislosti na vybraných bodech parametru a.

Pokud se s=a. Pak F není definována a v grafu vznikají "modré zuby."

Detailní pohled na F(s)=1/(s-a) s parametrem a=1. Je dobře vidět, že se pro velká s velmi rychle blíží k nule zatímce funkce f , exponenciela se rychle blíží k nekonečnu.

Základní pravidlo počítání Laplaceovy transformace F nebo-li Lf

Platí:

L(u + v) = Lu + Lv

L(c v) = c Lv

kde c ..konstanta a u,v ..jsou funkce závislé na t

komplexní funkce L(f + ig) = F + iG >>> Lf = F , Lg = G (po částech)

TABULKA LAPLACEOVÝCH TRANSFORMACÍ :

tabuka je také zde

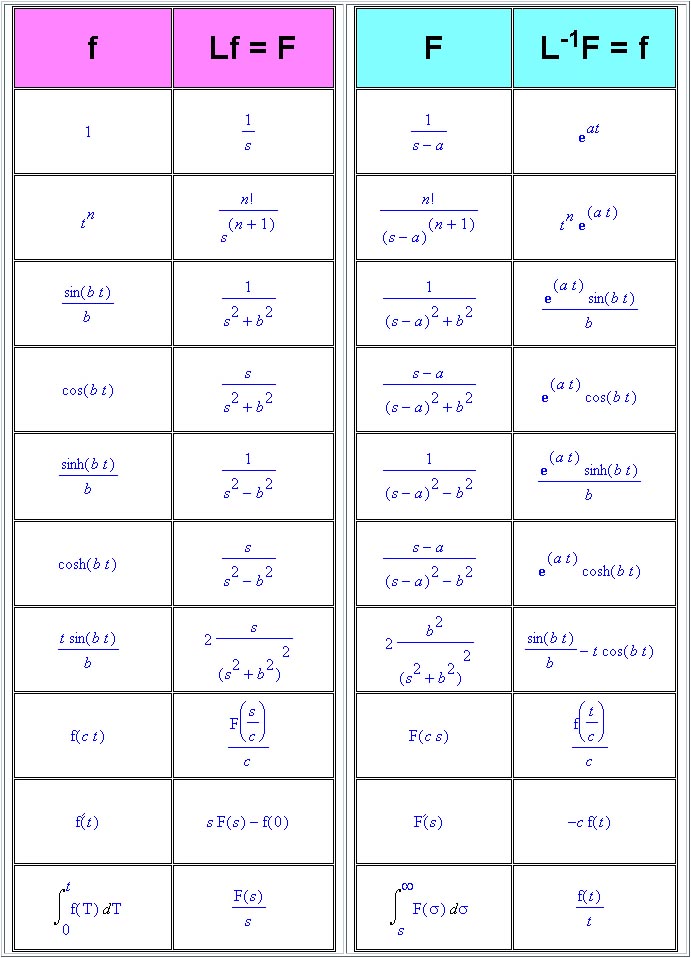
Příklady Laplaceových transformací s grafy funkcí:

Příklad 1:

Příklad 2

Animace v závislosti na parametru a

Příklad 3

Animace v závislosti na parametru a

Příklad 4

Animace v závislosti na parametru a

Příklad 5, komplexní funkce

Jedná se o funkci jedné komplexní proměnné, se kterou se pracuje jako s funkcí dvou reálných proměnný (x,i). V grafu se jedná o zobrazení funkce z komplexní roviny o souřadnicích (x,i) do prostoru.

Zobrazení je definováno takto:

místo původní

je použito

kde