![[Maple Plot]](images/reim2.gif)
Mocninne rady
Power series
![[Maple Plot]](images/reim2.gif)
Mocninnou radu definujeme v oboru komplexnich cisel jako
![sum(a[n]*(z-s)^n,n = 0 .. infinity)](images/mocninne_rady1.gif)
kde
z
,
s
jsou komplexni cisla a (
![]() ) je posloupnost komplexnich cisel.
s
se nazyva stred,
) je posloupnost komplexnich cisel.
s
se nazyva stred,
![]() jsou koeficienty mocninne rady. Bude nas zajimat, pro jaka
z
rada konverguje. Plati veta, ze pro kazdou mocninnou radu existuje jednoznacne urcene kladne realne cislo (nebo
jsou koeficienty mocninne rady. Bude nas zajimat, pro jaka
z
rada konverguje. Plati veta, ze pro kazdou mocninnou radu existuje jednoznacne urcene kladne realne cislo (nebo
![]() ) R takove, ze rada konverguje pro vsechna
z
pro nez
) R takove, ze rada konverguje pro vsechna
z
pro nez
![]() a diverguje pro vsechna
z
pro nez
a diverguje pro vsechna
z
pro nez
![]() > R. Toto cislo nazveme
polomer konvergence
.
> R. Toto cislo nazveme
polomer konvergence
.
Pokud existuje limita posloupnosti
![L = Limit(abs(a[n])^(1/n),n = infinity)](images/mocninne_rady7.gif) , je polomer konvergence
, je polomer konvergence
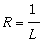 . Je-li L=0, je R=
. Je-li L=0, je R=
![]() , je-li L=
, je-li L=
![]() , je R=0.
, je R=0.
Power serie is defined in complex numbers as
![sum(a[n]*(z-s)^n,n = 0 .. infinity)](images/mocninne_rady11.gif)
where
z
,
s
are complex numbers and (
![]() ) is complex serie.
s
is called center,
) is complex serie.
s
is called center,
![]() coefficients of the power serie. The question is for what values of
z
does the serie converg. It can be proven that every power serie has associated unique positive real number (or
coefficients of the power serie. The question is for what values of
z
does the serie converg. It can be proven that every power serie has associated unique positive real number (or
![]() ) R such that the serie convergs for every
z
such that
) R such that the serie convergs for every
z
such that
![]() and divergs for every
z
such that
and divergs for every
z
such that
![]() > R.
We'll call this number the
convergence radius
.
> R.
We'll call this number the
convergence radius
.
Let's assume that the following limit exists:
![L = Limit(abs(a[n])^(1/n),n = infinity)](images/mocninne_rady17.gif) . Convergence radius can then be expressed as
. Convergence radius can then be expressed as
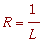 . If L=0 then R=
. If L=0 then R=
![]() , if L=
, if L=
![]() then R=0.
then R=0.
Podivejme se, jak se chova mocinna rada
![]() :
:
Let's see how does this power serie behave:
![]() :
:
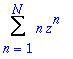 | ![[Maple Plot]](images/mocninne_rady27.gif)
|
![[Maple Plot]](images/reim1.gif)
| |
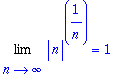
Dle teorie tedy tato rada konverguje pro z<1, coz odpovida i udajum na animovanem grafu.
According to the theory, this serie convergs for z<1, which is indeed what we can see at the plot.
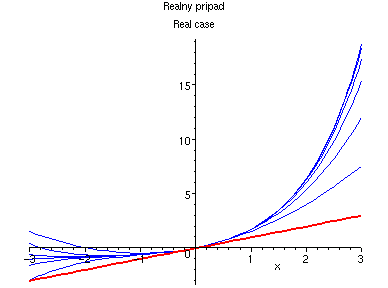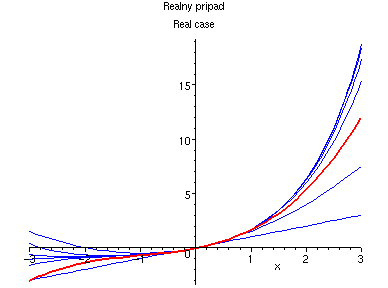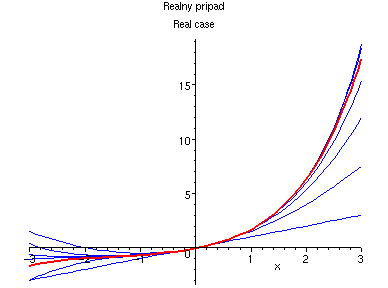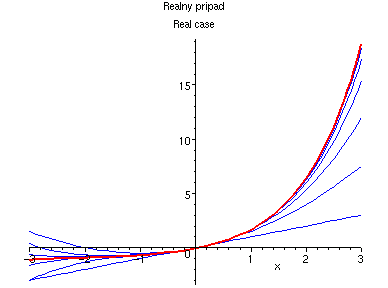
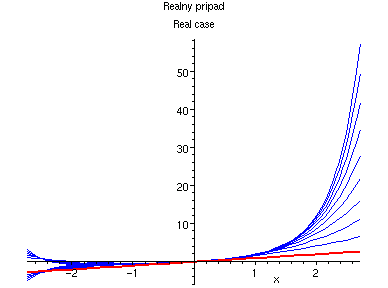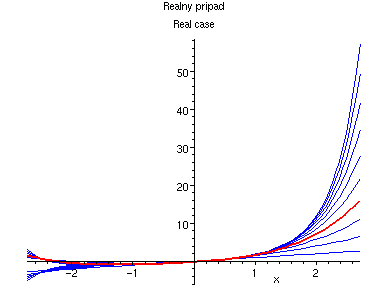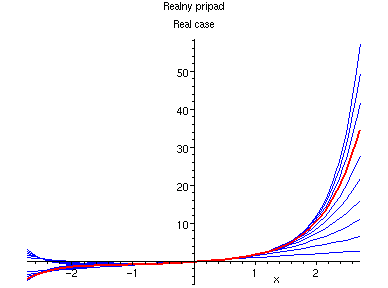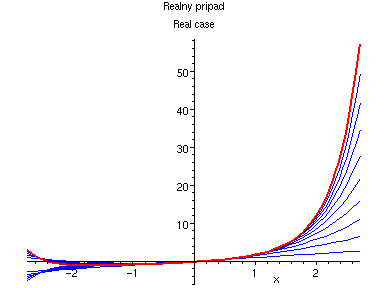
Exponenciela:
The exponential function:
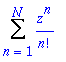 | 
|
![[Maple Plot]](images/reim2.gif)
| |
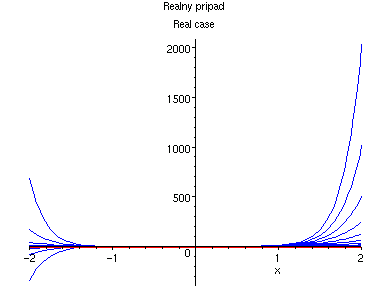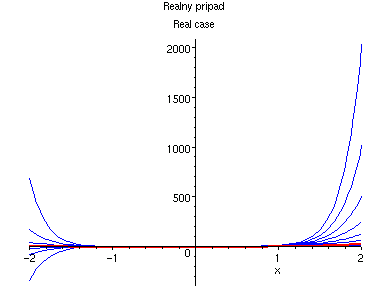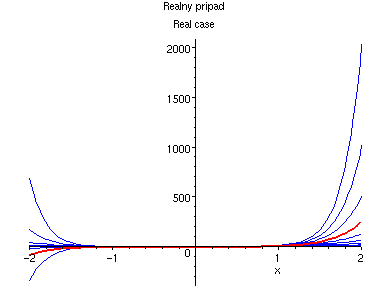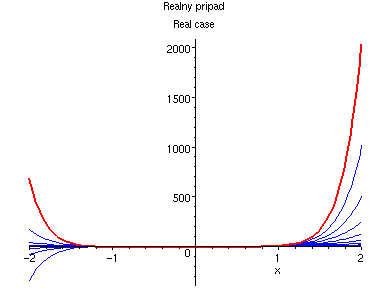
Nasledujici rada ma polomer konvergence 1 a obor konvergenze nelze rozsirit, rada osciluje ve vsech bodech jednotkove kruznice:
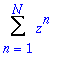 | 
|
![[Maple Plot]](images/reim3.gif)
| |
A tato rada ma polomer konvergence e:
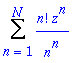 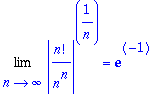 | 
|
![[Maple Plot]](images/reim4.gif)
| |
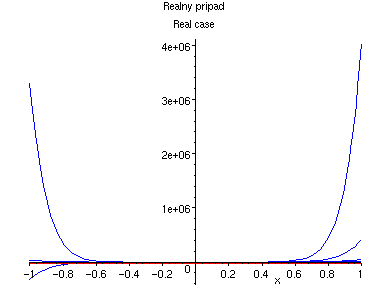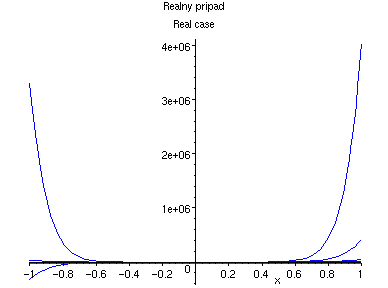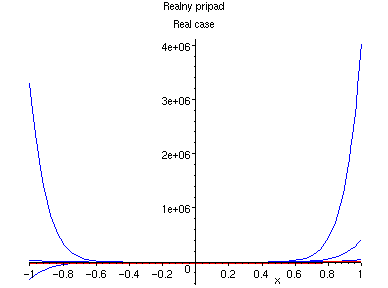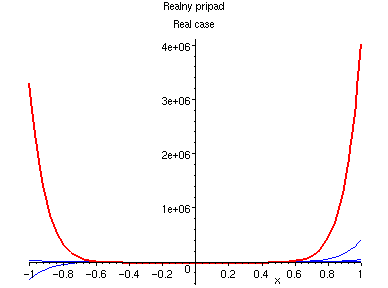
Tato rada nikde nekonverguje:
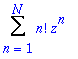 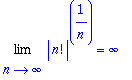 | 
|
![[Maple Plot]](images/reim5.gif)
| |