Maple nám to spočítá

Na začátku provedeme restart kernelu a načteme potřebné funkce z knihoven.

>	restart; with(plots,display); with(plottools,[ellipse]); with(DEtools,odeadvisor);

Diferenciální rovnici přiřadíme do proměnné.

>	eq := m*diff(x(t),t$2)+h*diff(x(t),t)+k*x(t)=0;

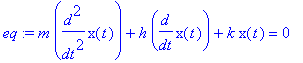
Než začneme počítat, uložíme si ještě do proměnných rovnice obecných počátečních podmínek pro polohu a rychlost, které použijeme při řešení rovnice.

>	InitX := x(0)=x0; InitV := D(x)(0)=v0;

Nyní již máme vše připraveno, proto můžeme přistoupit k samotnému řešení rovnice pomocí funkce 'dsolve'. Právě teď využijeme výhody počítačového zpracování a necháme si vyjádřit zcela obecné řešení s počátečními podmínkami i parametry rovnice ve formě proměnných bez přiřazené hodnoty. To nám později umožní tyto hodnoty měnit bez opětovného řešení rovnice. Při 'ručním' řešní by se o stejný postup pravděpodobně nikdo nepokoušel (přinejmenším ne dobrovolně :-) ) a snažil by se výraz alespoň nějak průběžně zjednodušovat.

>	solution := dsolve({eq,InitV,InitX});

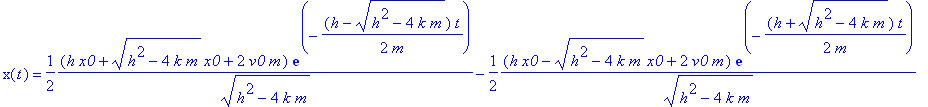
Když už máme řešení (ať už vlastní nebo vypočítané Maplem), můžeme si ověřit, jestli je správně, tedy jestli skutečně řeší původní rovnici. K tomu slouží funkce 'odetest'. Pokud výraz předaný jako první parametr řeší rovnici předanou ve druhém parametru, funkce vrací nulu.

>	odetest(solution,eq);

Nakonec ještě z řešení uloženého v proměnné jako rovnice uděláme fukci, její první derivaci uložíme jako rychlost a máme spočítáno. Samořejmě, že celá záležitost není až tak složitá a rovnice jde řešit i 'ručně', ale tento postup je přece jenom poněkud pohodlnější :-).

>	x := unapply(rhs(solution),t): v := D(x): a := D(v):

Když máme řešení v obecném tvaru, mužene nyní do proměnných uložit potřebné hodnoty, aby byly použity pro vykreslování v další části. Pokud chceme parametry nebo počáteční podmínky změnit, stačí se prostě vrátit k tomuto segmentu, hodnoty změnit a segment znovu provést. Poslední podmínka nám slouží  k ošetření drobné nepříjemnosti s dělením nulou. Správně by pro tuto situaci rovnice vyžadovala samostatné řešení, které je poměrně jednoduché, ale vzhledem k tomu, že nám jde především o grafické znázornění, spokojíme se s tímto postupem. Díky tomu máme možnost sledovat změny řešení pouze úpravou následujících hodnot bez nutnosti opětovného řešení rovnice.

>	m := 1:    # hmotnost h := 1/7:  # koeficient tlumeni k := 1:    # tuhost x0 := 10:  # pocatecni vychylka v0 := 0:   # pocatecni rychlost if (h^2 = 4*m*k) then   h := h + 0.000000001: end if:

Boolovská proměnná anim (hodnoty true/false) nastavuje, zda bude součástí výsledného zobrazení také animace. Příprava vykreslování je bez animace pochopitelně výrazně rychlejší.

>	anim := true:

Dále musíme nastavit parametry zobrazení a animace. Proměnná 'step' určuje interval mezi jednotlivými snímky animace. Nemá vliv na přesnost výpočtu (nejedná se o interval pro numerické řešení), protože rovnici máme vyřešenou analyticky. Pouze ovlivňuje, jak plynulá animace bude. Proměnná 'MaxTime' určuje celkový čas, pro který bude zobrazen graf a animace. Ostatní proměnné nastavují meze zobrazení.

>	step := 0.5:       # krok animace MaxTime := 15:     # celkovy cas left:= -13:       # rozsahy zobrazeni right := MaxTime: low := -10: high := 11.5:

>

DrawVerticalSpring := proc(Sx, Sy, Ey, n, width, clr, t)   local     i, p, dx, dy, x, y, c, Ex;   Ex := Sx;   dx := (Ex - Sx) / n;   dy := (Ey - Sy) / n;   p[1]:= plot([ [Sx, Sy], [Sx+dx, Sy+dy] ], color=clr, thickness=t);   for i from 2 to n-1   do     x := Sx + dx*(i-1);     y := Sy + dy*(i-1);     p[i] := plot( [ [x,y],                     [x - width, y + dy*(1/4)],                     [x + width, y + dy*(3/4)],                     [x+dx, y+dy] ],                   color=clr, thickness=t );   end do;   p[n] := plot([[Ex-dx,Ey-dy], [Ex,Ey]], color=clr, thickness=t);   plots[display]( seq(p[i], i=1..n) ); end proc:

Nyní jsme se dostali k samotnému zobraní. Do proměnné p vykreslíme graf polohy, rychlosti a zrychlení a text. Pokud se má kreslit i animace, provede se cyklus, ve kterém do pole uložíme jednotlivé snímky animace. Tyto snímky poté složíme do sekvence a složíme s grafy polohy a rychlosti.
p := plot([x(t), v(t), a(t)], t=0..MaxTime, thickness=[2,1,1], color=[blue, green, gray]),
     plot([0.3*x(t)-8, 0.3*v(t)+5, t=0..MaxTime], color=red),
     TEXT([-8, -2], "modra - poloha"),
     TEXT([-8, -3], "zelena - rychlost"),
     TEXT([-8, -4], "seda - zrychleni"),
     TEXT([-8, 2], "fazovy diagram"):
if (anim=true) then
  for i from 0 to MaxTime/step do
    pos := x(step*i);
    vel := v(step*i);
    acc := a(step*i);
    spring[i] := DrawVerticalSpring(-2, pos, 11.5, 20, 0.3, black, 2);
    phase[i] := ellipse([0.3*pos-8,0.3*vel+5], 0.15,0.15, color=red, filled=true):
    blob[i] := ellipse([-2,pos], 0.4,0.4, color=black, filled=true):
    blobPos[i] := ellipse([step*i,pos], 0.15,0.15, color=blue, filled=true):
    blobVel[i] := ellipse([step*i,vel], 0.15,0.15, color=green, filled=true):
    blobAcc[i] := ellipse([step*i,acc], 0.15,0.15, color=gray, filled=true):
  od:
  springA := display([seq(spring[i], i=0..MaxTime/step)], insequence=true):
  phaseA := display([seq(phase[i], i=0..MaxTime/step)], insequence=true):
  blobA := display([seq(blob[i], i=0..MaxTime/step)], insequence=true):
  PosA := display([seq(blobPos[i], i=0..MaxTime/step)], insequence=true):
  VelA := display([seq(blobVel[i], i=0..MaxTime/step)], insequence=true):
  AccA := display([seq(blobAcc[i], i=0..MaxTime/step)], insequence=true):
  disp := p, springA, phaseA, blobA, PosA, VelA, AccA:
else
  disp := p:
end if:

Vše je hotovo a připraveno pro zobrazení. Pokud jste nastavili proměnnou 'anim' na true, mužete tlačítkem play spustit animaci kmitů. Tlačítky s dvojitou šipkou lze také nastavit rychlost animace. Pokud animace není plynulá, je třeba zvýšit rychlost zobrazování snímků. Jestliže však zároveň nechcete zvýšit celkovou rychlost přehrávání, musíte snížit hodnotu proměnné 'step'.

>	display(disp, scaling=constrained, view=[left..right,low..high]);