Jak na to
Při sestavování pohybové rovnice vyjdeme z druhého Newtonova zákona:
 .
.
Pokud polohu jako funkci času označíme 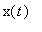 , můžeme rovnici přepsat do tvaru
, můžeme rovnici přepsat do tvaru
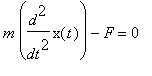
V případě lineárního oscilátoru můžeme sílu vyjádřit jako přímo uměrnou aktuální výchylce, odpovídající koeficient označíme 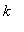 . Síla směřuje vždy směrem do klidové polohy, to jest má opačné znaméno než výchylka. Budeme se zajímat o tlumení, které je přímo úměrné rychlosti pohybu, což je ve spoustě fyzikálních situací v podstatě splněno. Koeficient tlumení označíme
. Síla směřuje vždy směrem do klidové polohy, to jest má opačné znaméno než výchylka. Budeme se zajímat o tlumení, které je přímo úměrné rychlosti pohybu, což je ve spoustě fyzikálních situací v podstatě splněno. Koeficient tlumení označíme 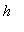 . Konečná podoba naší rovnice tedy je
. Konečná podoba naší rovnice tedy je

Vidíme, že se jedná o rovnici bez nezávislé proměnné. Řešení klasickým způsobem pouze naznačíme, protože ve srovnání s použitím možností Maplu se jedná o postup poněkud zdlouhavý. Poslouží nám ovšem jako dobrá ilustrace toho, kolik práce mohou matematické programy ušetřit :-).
I když nápověda Maplu navrhuje jiný postup, pro názornost bych použil následující. Na základě rovnice napíšeme chrakteristický polynom:
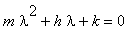 .
.
Jeho řešení bude pochopitelně záviset na hodnotách koeficientů. Tím se řešení rozdělí na tři případy, které odpovídají i třem různým fyzikálním situacím. Pokud  , jedná se o mezní případ 'optimálního tlumení' (viz například tlumiče pérování automobilů a motocyklů).
, jedná se o mezní případ 'optimálního tlumení' (viz například tlumiče pérování automobilů a motocyklů). 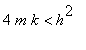 je případ kritického tlumení, kdy je tlumení tak veliké, že návrat do klidové polohy trvá déle než v prvním případě. Poslední možností je
je případ kritického tlumení, kdy je tlumení tak veliké, že návrat do klidové polohy trvá déle než v prvním případě. Poslední možností je 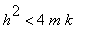 , což je klasické tlumené kmitání. V každém z případů bychom potom na základě kořenů chrakteristického polynomu nalezli fundamentální systém řešení. Tím ovšem není řešení hotové, ještě potřebujeme vzít v úvahu počáteční podmínky a na jejich základě stanovit koeficienty lineární kombinace jednotlivých funkcí fundamentálního systému... Jak říkám - ne zrovna málo práce. Takže pokud se vám nechce stejně jako mně, zkusme se podívat, jak nám s tím pomůže Maple :-).
, což je klasické tlumené kmitání. V každém z případů bychom potom na základě kořenů chrakteristického polynomu nalezli fundamentální systém řešení. Tím ovšem není řešení hotové, ještě potřebujeme vzít v úvahu počáteční podmínky a na jejich základě stanovit koeficienty lineární kombinace jednotlivých funkcí fundamentálního systému... Jak říkám - ne zrovna málo práce. Takže pokud se vám nechce stejně jako mně, zkusme se podívat, jak nám s tím pomůže Maple :-).
![[Maple Plot]](oscilatorimg/oscilator1.gif)
![[Maple Plot]](oscilatorimg/oscilator2.gif)
![[Maple Plot]](oscilatorimg/oscilator3.gif)
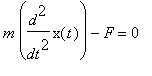

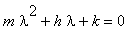 .
. , jedná se o mezní případ 'optimálního tlumení' (viz například tlumiče pérování automobilů a motocyklů).
, jedná se o mezní případ 'optimálního tlumení' (viz například tlumiče pérování automobilů a motocyklů). 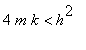 je případ kritického tlumení, kdy je tlumení tak veliké, že návrat do klidové polohy trvá déle než v prvním případě. Poslední možností je
je případ kritického tlumení, kdy je tlumení tak veliké, že návrat do klidové polohy trvá déle než v prvním případě. Poslední možností je 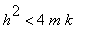 , což je klasické tlumené kmitání. V každém z případů bychom potom na základě kořenů chrakteristického polynomu nalezli fundamentální systém řešení. Tím ovšem není řešení hotové, ještě potřebujeme vzít v úvahu počáteční podmínky a na jejich základě stanovit koeficienty lineární kombinace jednotlivých funkcí fundamentálního systému... Jak říkám - ne zrovna málo práce. Takže pokud se vám nechce stejně jako mně, zkusme se podívat, jak nám s tím pomůže Maple :-).
, což je klasické tlumené kmitání. V každém z případů bychom potom na základě kořenů chrakteristického polynomu nalezli fundamentální systém řešení. Tím ovšem není řešení hotové, ještě potřebujeme vzít v úvahu počáteční podmínky a na jejich základě stanovit koeficienty lineární kombinace jednotlivých funkcí fundamentálního systému... Jak říkám - ne zrovna málo práce. Takže pokud se vám nechce stejně jako mně, zkusme se podívat, jak nám s tím pomůže Maple :-).![[Maple Plot]](oscilatorimg/oscilator23.gif)