Druhá derivace a její vliv na konVexnot a konkÁvnost; o definičních oborech.

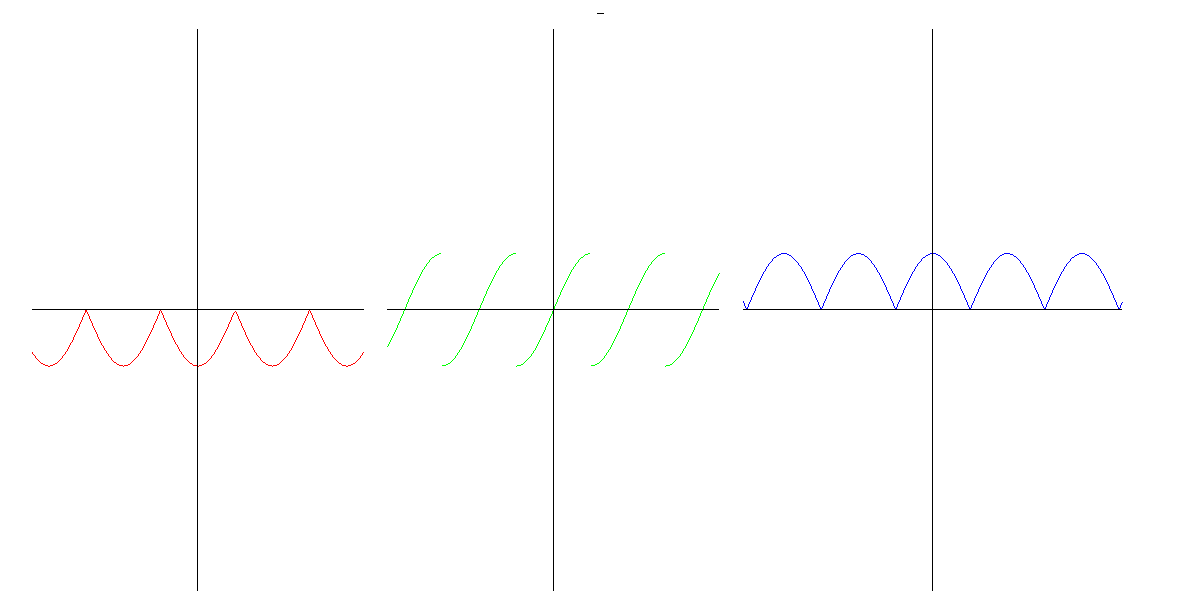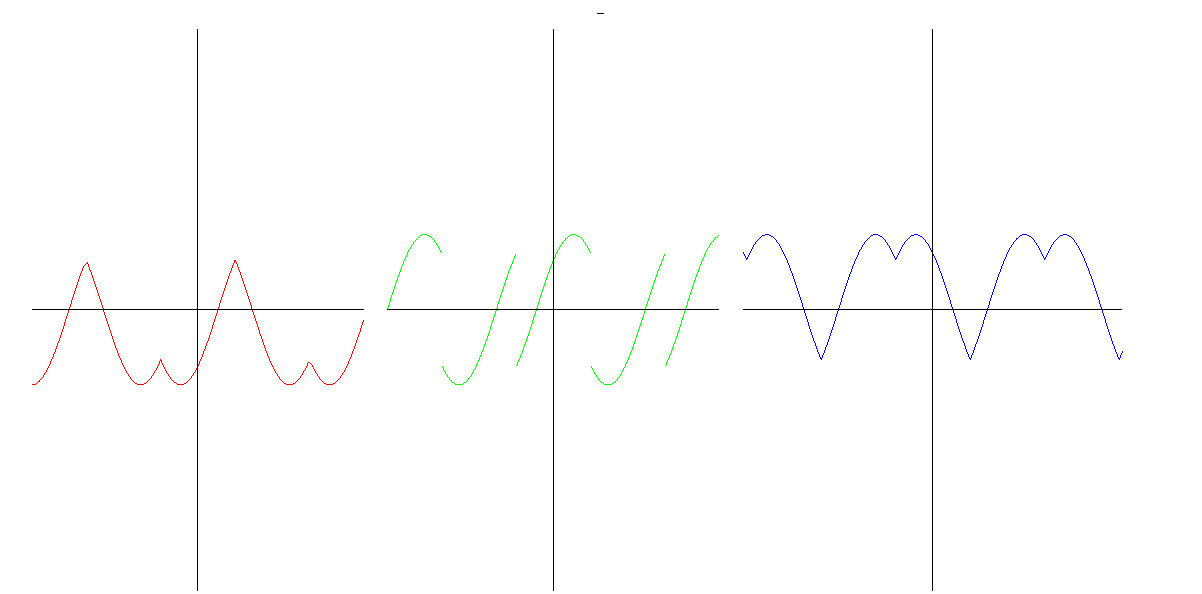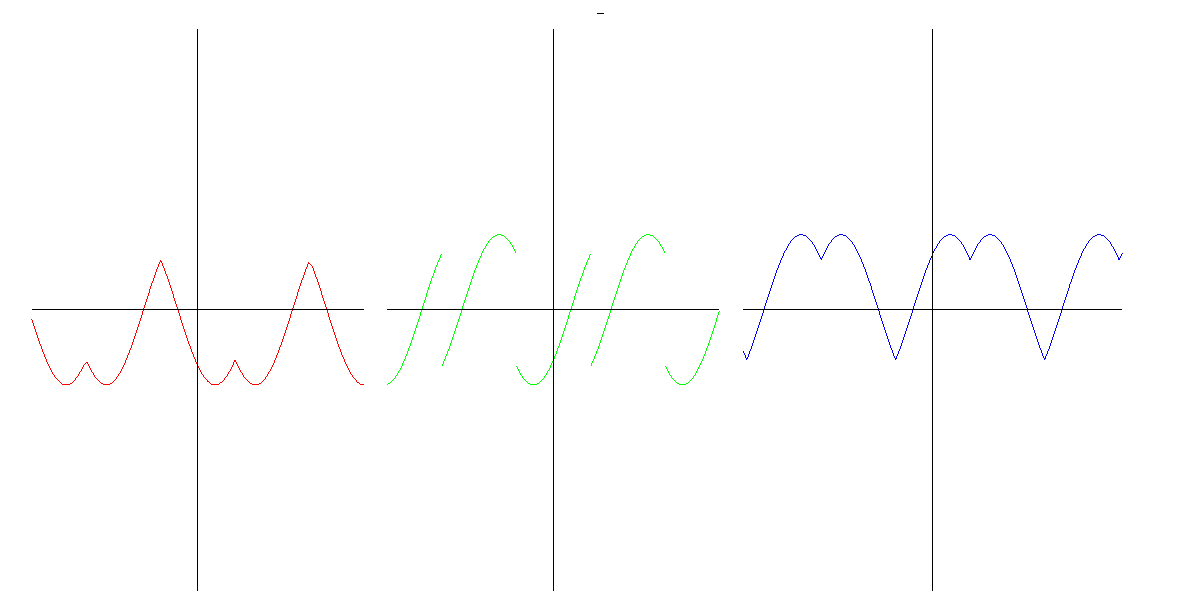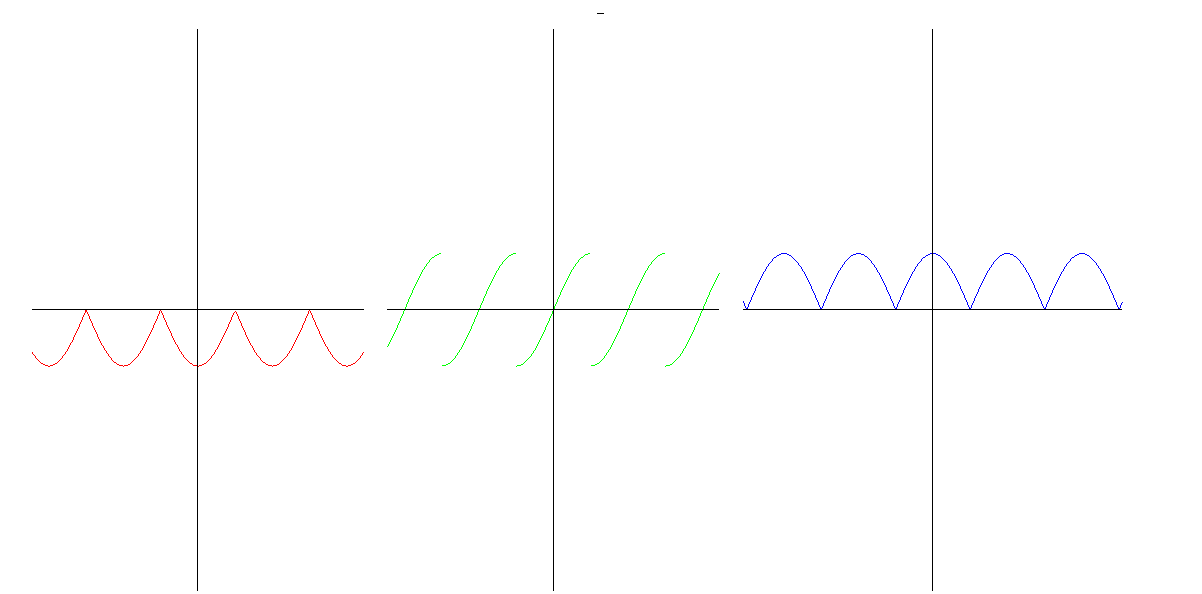
Před chvílí jsme se bavili o vztahu konvexity a stoupání derivace. Kdy však derivace stoupá? Pokud má derivaci (tedy pokud existuje druhá derivace původní funkce), pak tato musí být kladná. Platí tedy implikace: pokud druhá derivace existuje a je kladná, pak funkce je konkávní. Duálně pro konkávnost (záporná druhá derivace). To ale nevylučuje i jiné možnosti, kdy může být funkce konvexní, konkávní (neexistující derivace apod.). Na grafu vidíme funkci, její derivaci a druhou derivaci (odleva doprava). Funckce je konvexní na intervalech, na nichž je druhá derivace kladná, ale pozor! Není konvexní na celém definičním oboru, jen na intervalech mezi "zuby". Prohlédni si hodnoty první a druhé derivace v těchto zubech (ano, neexistuje tam, jelikož derivace zleva a derivace zprava jsou tam různé). Zkus najít funkci, která má "zub" (místo, na němž jesou různé derivace zleva a zprava, jejich definice je stejná jako u obvyklé derivace, akorát místo běžné limity je limita zleva, resp. zprava) a přesto je na intervalu, který tento zub obsahuje jako svůj vnitřní (rozuměj nikoli krajní) bod a přesto je na tomto intervalu konvexní nebo konkávní.

Na tomto obrázku je navíc vidět, že musíme dávat pozor na definiční obor a zrakový názor nás může trochu zmást. Podívej se na druhou derivaci v "zubech". Řeklo by se "Ano, ano, zleva to vypadá na nulu, zprava to vypadá na nulu, levá limita je stejná jako pravá, takže máme i celkovou limitu, derivace je limita, takže to tam má nulovou druhou derivaci."Není to pravda! Druhá derivace je derivace prvé derivace, abychom mohli prvou derivaci derivovat v bodě, musí tento bod být uvnitř definičního oboru (nebo na kraji, pokud se spokojíme s jednostrannou derivací), tedy definiční obor derivace bude podmnožina definičního oboru derivované funkce (možnost, že jsou tyto oobory stejné tím nevylučujeme), nikdy však nemůže být větší. Tomu se totiž říká "tzv. chybné zvětšení definičního oboru" :-) Příjemné počítání.