Klainova láhev

Autor: Vladimír Šišma
Datum: září 2001

Obsah

• Zadání
• Pojmy a definice
  • Co je Klainova láhev ... náznak definice
  • Topologie ... co to je
  • Definice Klainovy láhve ... matematická definice
  • Vlastnosti Klainovy láhve
• Řešení ... zdrojový text programu Maple (soubor "klain_src_mws")
  • Zajímavé postřehy ... čeho si všimnout
  • Obrázky ... to nejefektnější v tomto textu
• Tento text

Zadání

Zobrazte "Klainovu láhev" (viz dále) v prostoru E⁴ (,což je klasický geometrický čtyřrozměrný prostor - např. tři prostorové souřadnice a jedna časová). Výsledek neboli zobrazení, které bude znázorněno animací, bude přesně popisovat vztah mezi těmito prostory.

Pojmy a definice

Náznak definice: (Klainova láhev)
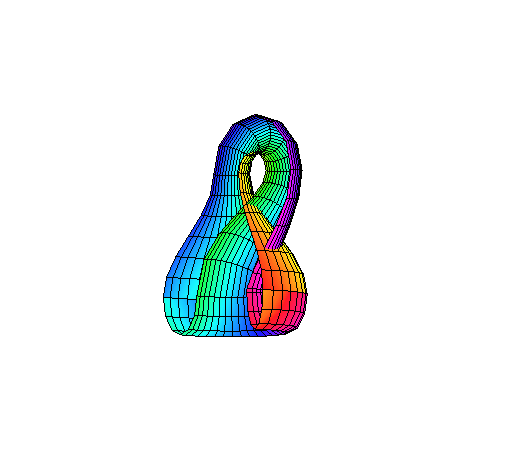
Klainovu láhev si můžeme představit jako roličku z papíru, jejíž konce napojíme "opačně" (viz obrázek 1 níže), než bychom je napojili přirozeným způsobem, tj. jako pneumatiku (viz obrázek 2 níže).

Obrázek 1

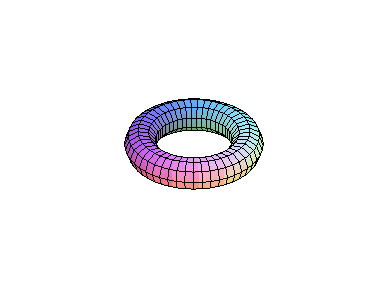
Obrázek 2

Pojem: (Topologie)
Topologie je struktura, která se definuje ve spojení s nějakou nosnou množinou (prostorem, ten pak nazýváme topologickým prostorem), a určuje takové vlastnosti prostoru jako jsou souvislost, spojitost a podobné.
Zobrazení mezi dvěma topologickými prostory, které topologii zachovává (vytvořit takové zobrazení je účelem této úlohy), musí splňovat takové vlastnosti jako, obraz souvislé oblasti (respektive spojité křivky) je opět souvislá oblast (respektive spojitá křivka), tj. zachovává souvislost i spojitost.

Definice: (Klainova láhev)
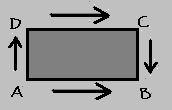
Definovat Klainovu láhev lze mnoha izomorfnímy (totožnými) způsoby, jeden z nich následuje. Z matematického hlediska je Klainova láhev čtverec (označme jej ABCD - podmnožina R² (R značí reálná čísla) se standardní topologoií, např. kartézský součin uzavřených intervalů [0,1]x[0,1]) se změněnou topologií na okrajích, uvnitř ponecháme topologii standardní. Hrany AB, CD ztotožníme (nebo jinak řečeno spojíme je tak, že "splynou" - stanou se totožnými; tímto krokem se samozřejmě změní i souvislost neboli topologie) "souhlasným" směrem, tj. bod A s bodem D, B s C a vnitřek úseček doztotožníme přirozeně podle krajních bodů, tak dostaneme už zmíněnou "papírovou roličku". Dále hrany BC, AD ztotožníme "opačným" směrem, tj. bod A s bodem C, B s D (ztotožnění do kříže) a vnitřek úseček opět doztotožníme přirozeně podle krajních bodů. Výsledkem je pak Klainova láhev (viz obrázek 1 výše). Ztotožnění hran naznačí obrázek 3 níže. Šipky ukazující stejným směrem naznačují "souhlasné" ztotožnění, šipky ukazující opačným směrem "opačné" ztotožnění.

Obrázek 3

Vlastnosti: (Klainova láhev)
Takovýto objekt má několik neobvyklých vlastností:

• plocha nemá klasické dvě strany (např. list papíru takové dvě strany má), ale jen jednu. Tzn., že pokud budeme po Klainově láhvi putovat prstem, můžeme se dostat do libovolného bodu plochy na obou tzv. "stranách" narozdíl od listu papíru.
• při pokusech takovou "opačně" napojenou papírovou roličku sestrojit dle obrázku 1 zjistíte, že to jde velmi špatně, protože Vám zavazí neprostupná hmota papíru. Zobrazení, které máme sestrojit, musí zachovávat topologii (viz topologie), tedy nesmí dojít ke křížení ploch, tj. porušení souvislosti (spojitosti). Toto může být argument, proč nám nebude stačit trojrozměrný prostor (tento fakt je striktně dokázán). Proto použijeme čtyřrozměrný prostor.

Definice: (prostor E⁴)
Označením E⁴ myslíme klasický geometrický nebo také euklidovský čtyřrozměrný prostor. Tj. R⁴ (R značí reálná čísla) se standardní topologií, metrikou (měření vzdáleností).

Řešení

Protože se budeme pohybovat ve čtyřrozměrném prostoru a Klainova láhev je dvourozměrná, budeme v animaci vidět pohybující se pásek - kružnici. Klainova láhev je navíc obarvena, aby bylo lépe vidět "opačné" napojení roličky. Vedle Láhve se zároveň zobrazuje část (příčné proužky) obarveného, stočeného a zkrouceného čtverce tak, že je dobře vidět "opačné" ztotožnění hran AD, BC (viz část matematická definice Klainovy láhve). "Souhlasné" ztotožnění pro jednoduchost naznačeno není. Zobrazované proužky čtverce v každém okamžiku odpovídají právě zobrazené kružnici - odpovídají si body právě stejných barev, takto jsme kýžené zobrazení přesně popsali a definovali. Výslednou animaci si prohlédněte níže. Následuje několik postřehů a pozorování.

K vygenerování animací a jiných obrázků byl použit matematický program Maple verze 6. Zdrojový kód k výpočtům najdete zde v originální podobě nebo v html podobě.

Postřehy

K lepšímu pochopení výsledku a většímu nadhledu nad problémem je dále uvedeno několik zajímavých postřehů a pozorování.

• Jak jsme už zmínili ve vlastnostech Klainovy láhve, nelze korektně realizovat zobrazení v třírozměrném prostoru. Jedno takové třírozměrné zobrazení dostaneme, když si u výsledné animace odmyslíme její "hloubku", tedy třetí prostorový rozměr. Jiné takové získáme projekcí animace přes čas, tj. nakreslíme si všechny postupně objevující se kružnice do jednoho času - na jeden papír, tato projekce je rovněž uvedena mezi obrázky. Správný výsledek se nám podaří vyrobit až při použití čtyř dimenzí, což je i náš případ.
• Doporučuji podrobněji prozkoumat, zda se "opačné" ztotožnění provedlo opravdu bez chyb. Jediný kritický okamžik, kde to je nejlépe vidět, nastává na konci animace. Je lepší si prohlédnout statické obrázky a prozkoumat, zda splynou ty samé barevné body jak na Láhvi, tak na čtverci. Jen mimochodem poznamenejme, "zkroucenému" čtverci se říká Moebiův list.

Obrázky

Níže se nachází výsledný hlavní obrázek. Co znázorňuje, popisuje celý tento text.

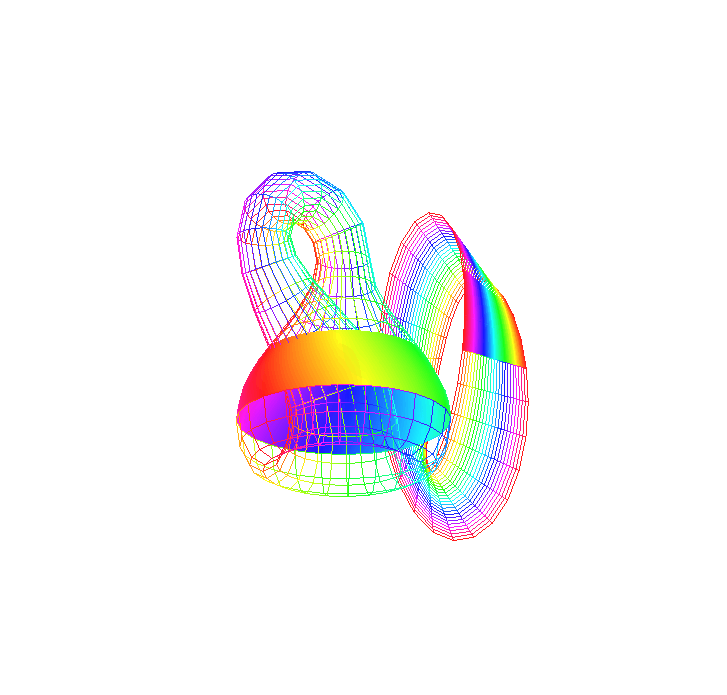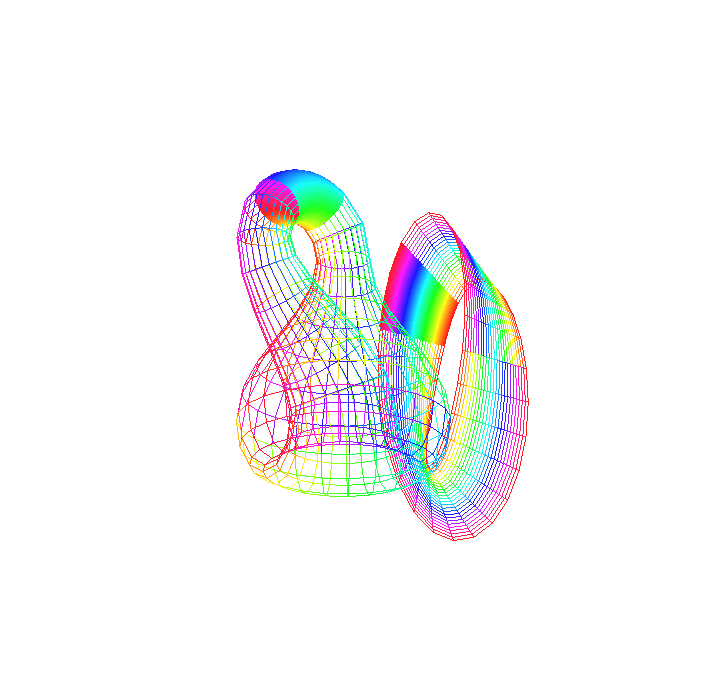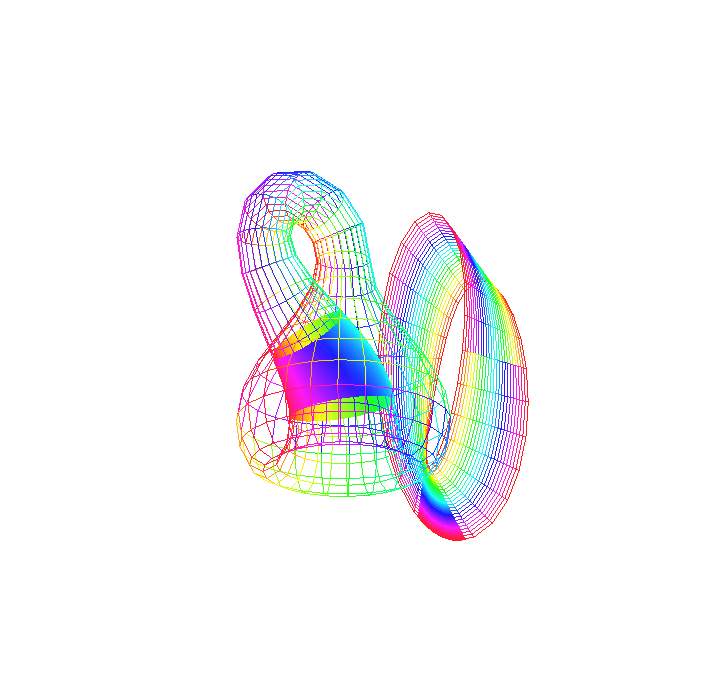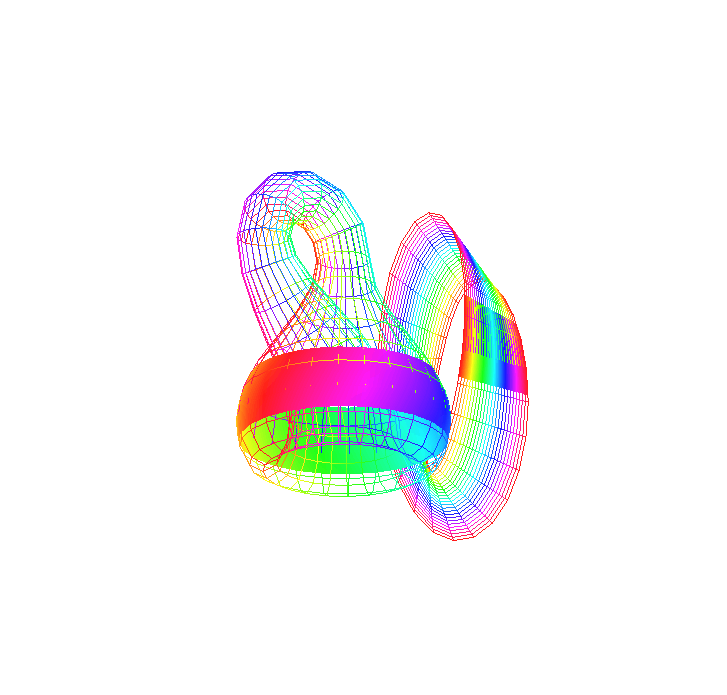
Klainova láhev - hlavní výsledek

Níže se nachází předešlá Klainova láhev jen vykreslená naráz (lze to nazvat projekcí přes časovou souřadnici). Pak zde také naleznete i rozříznutý exemplář.

Klainova láhev - projekce přes čas - řez středem

Klainova láhev - projekce přes čas - řez středem

Tento text

Tento text vznikl při příležitosti konání semináře Matematika na počítači pod vedením pana Doc. Pavla Pyriha CSc. na Matematicko-fyzikální fakultě Univerzity Karlovy v Praze.