populace
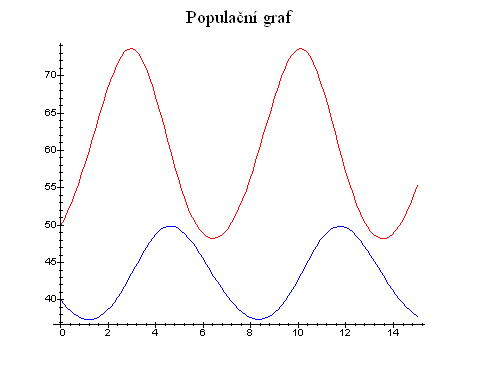
Modrá - dravci
Soustavu diferenciálních rovnic
x' = ax -bxy
y' = -cy +dxy
nazýváme termínem dravec-kořist.
Proč? To vyplývá z charakteru soustavy.
To, že se kořist (např;. zajíci) množí, můžeme znázornit rovnicí
x'=ax kde a>0 je konstanta (faktor množení).
Dravci (např. lišky) bez potravy vymírají
y'=-cy
kde c>0 je konstanta (faktor úhynu).
A faktor že dravec potká lišku
hxy
kde h>0 je konstanta (b pro kořist, d pro dravce).
Dále troška matematiky nikomu neuškodí...
K názorné demonstraci zkonstruujeme několik grafů s měnícími se parametry.
x' = 1,3x -0,03xy
y' = -0,6y +0,01xy
Nejdříve malé vysvětlení, abychom následujícím grafům lépe rozuměli.
| Velikost populace |
 |
Červená - koříst Modrá - dravci |
| Velikost populace kořisti |
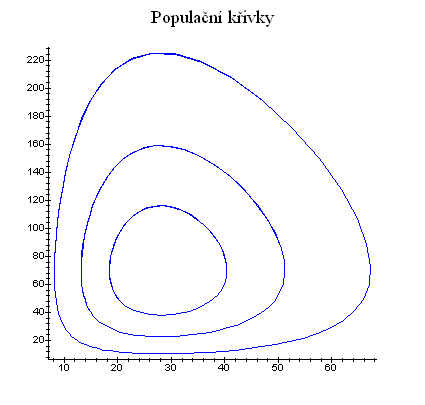 |
Jednotlivé kruhy představují cykly populačního grafu - vztah počtu kořisti a dravců. Jak víme, počet dravců a kořisti s časem osciluje, což se projeví v uzavřenosti křivky. Různé křivky představují různé počáteční stavy počtu kořisti a dravců při zachování parametrů soustavy rovnic (v tomto příkladě představuje od vnějšího kruhu počáteční stav [dravec, kořist] [50, 20], [40, 15], [30, 10]). |
Následující obrázky ukazují jak se populační graf mění se změnou parametrů a, b, c a d.
| Změna parametru a | Změna parametru b |
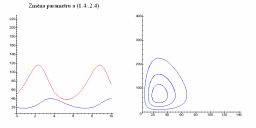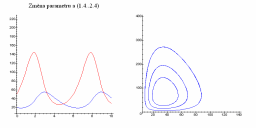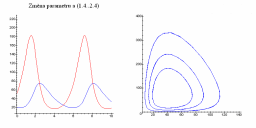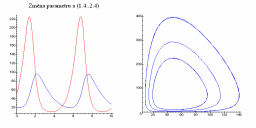 |
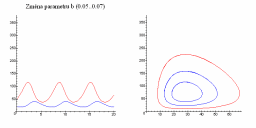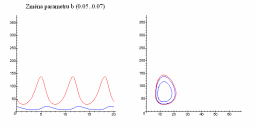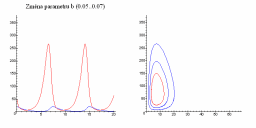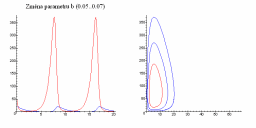 |
| Změna parametru c | Změna parametru d |
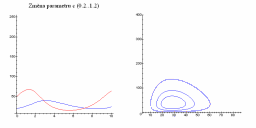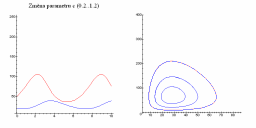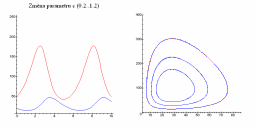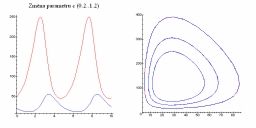 |
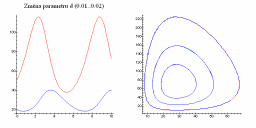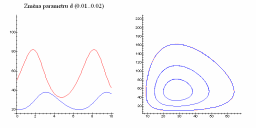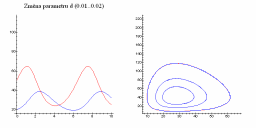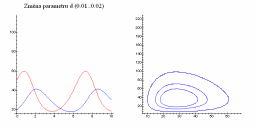 |
| Změna a/b | Změna c/d |
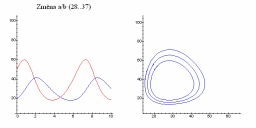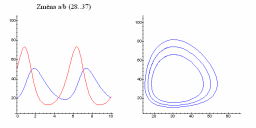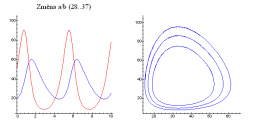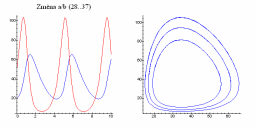 |
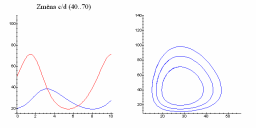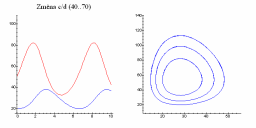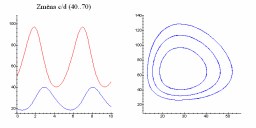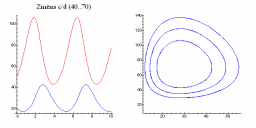 |
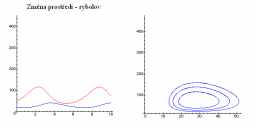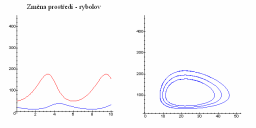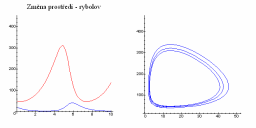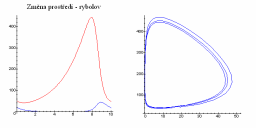
Rovnice můžeme pozměnit tak, abychom mohli simulovat vnější zásahy do systému (např. rybolov při simulaci typu žralok-rybičky kdy se jako narušující faktor jeví rybáři). Řekněme, že rybáři vyloví všechny ryby z daného dílu životního prostředí (nějaké![]() ). Pak budou mít rovnice tvar:
). Pak budou mít rovnice tvar:
x' = ax -bxy -![]() x
x
y' = -cy +dxy -![]() y
y
Nové průměry se pak změní:
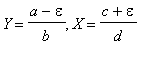
| Změna prostředí |
 |